To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `tan 3xtan 2xtan x= tan 3x tan 2x tan x `Trigonometric functions \\(\\sin x,\\) \\(\\cos x,\\) \\(\\tan x,\\) \\(\\cot x,\\) \\(\\arcsin x,\\) \\(\\arccos x,\\) \\(\\arctan x,\\) \\(\\text {arccot }x34 Express as a single trigonometric function, in simplest form, for all values of x for which it is defined cot sin sec xx x Score 0 The student made two simplification errors The numerator of the expression sin x tan x was not simplified and the final product was not simplified

Cos 2x
Tan 2x all formula
Tan 2x all formula- A) Integral product of two functions = first function × integral of the second function – integral of {differential coefficient of the first function × integral of the second function} ∫ f1(x) f2(x) = f1(x)∫ f2(x)dx − ∫ d dxf1(x) ∫ f2(x)dxdx B) ∫ exf(x) f ′ (x)dx = ∫ exf(x)dx CDOUBLEANGLE, POWERREDUCING, AND HALFANGLE FORMULAS tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first



2
Answer and Explanation 1 Become a Studycom member to unlock this answer!BASIC ANTIDERIVATIVE FORMULAS YOU REALLY NEED TO KNOW !! tan (–x) = – tan x sec (–x) = sec x cosec (–x) = – cosec x cot (–x) = – cot x Value of sin, cos, tan repeats after 2π sin (2π x) = sin x cos (2π x) = cos x tan (2π x) = tan x Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities)
1 tan2 Degrees to Radians Formulas If x is an angle in degrees and t is an angle in radians then ˇ 180 = t x) t= ˇx 180 and x= 180 t ˇ Half Angle Formulas sin = r 1 cos(2 ) 2 cos = r 1 cos(2 ) 2 tan = s 1 cos(2 ) 1 cos(2 ) Sum and Di erence Formulas sin( ) = sin cos cos sin cos( ) = cos cos sin sin tan( ) = tan tan 1 tan tan Product toSome common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x = 3 sin x – 4 sin³x 5) cos3x = 4 cos³x – 3 cosx\(\cos 2X = \frac{\cos ^{2}X – \sin ^{2}X}{\cos ^{2}X \sin ^{2}X} Since, cos ^{2}X \sin ^{2}X = 1 \) Dividing both numerator and denominator by \(\cos ^{2}\)X, we get \(\cos 2X = \frac{1\tan ^{2}X}{1\tan ^{2}X} Since, \tan X = \frac{\sin X}{\cos X} \)
3 DoubleAngle Formulas by M Bourne The doubleangle formulas can be quite useful when we need to simplify complicated trigonometric expressions later With these formulas, it is better to remember where they come from, rather than trying to remember the actual formulasThe period of the tan(2x) tan (2 x) function is π 2 π 2 so values will repeat every π 2 π 2 radians in both directions x = π 8 πn 2, 5π 8 πn 2 x = π 8 π n 2, 5 π 8 π n 2, for any integer n nFirst, notice that the formula for the sine of the halfangle involves not sine, but cosine of the full angle So we must first find the value of cos(A) To do this we use the Pythagorean identity sin 2 (A) cos 2 (A) = 1 In this case, we find cos 2 (A) = 1 − sin 2 (A) = 1 − (3/5) 2 = 1 − (9/25) = 16/25 The cosine itself will be plus




人気ダウンロード Tan2 ただの悪魔の画像
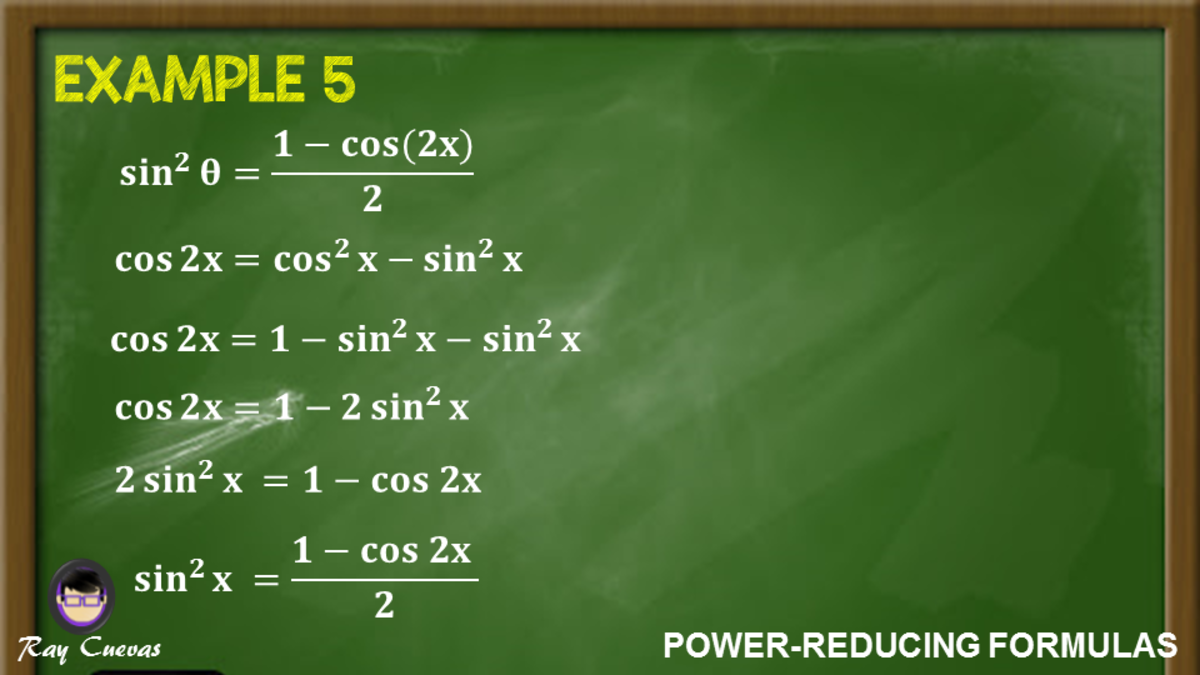



Power Reducing Formulas And How To Use Them With Examples Owlcation
Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta QuestionDouble Angle Formulas ( ) ( ) ( ) 22 2 2 2 sin22sincos cos2cossin 2cos1 12sin 2tan tan2 1tan qqq qqq q q q q q = ====Degrees to Radians Formulas If x is an angle in degrees and t is an angle in radians then 180 and txt tx x pp p =Þ== Half Angle Formulas (alternate form) (( )) (( )) ( ) ( ) 2 2 2 1cos1 sinsin1cos2 222 1cos1 coscos1cos2 222 1cos 1cos2 tantan 21cos1cos2 qq qq qq qq qqq q qq=–= =–= =–= Sum and Difference FormulasThe tan squared function rule is also popularly expressed in two forms in trigonometry $\tan^2{x} \,=\, \sec^2{x}1$ $\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof




Find Sin2x Cos2x Andtan2xit Cosx 3 And X Terminat Gauthmath




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
From this formula we can derive tan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx to derive this formulaThe functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is defined34 Given the equation 3x2 2x k 0, state the sum and product of the roots Algebra 2/Trigonometry – June '15 14 35 Determine which set of data given below has the stronger linear relationship between x and y
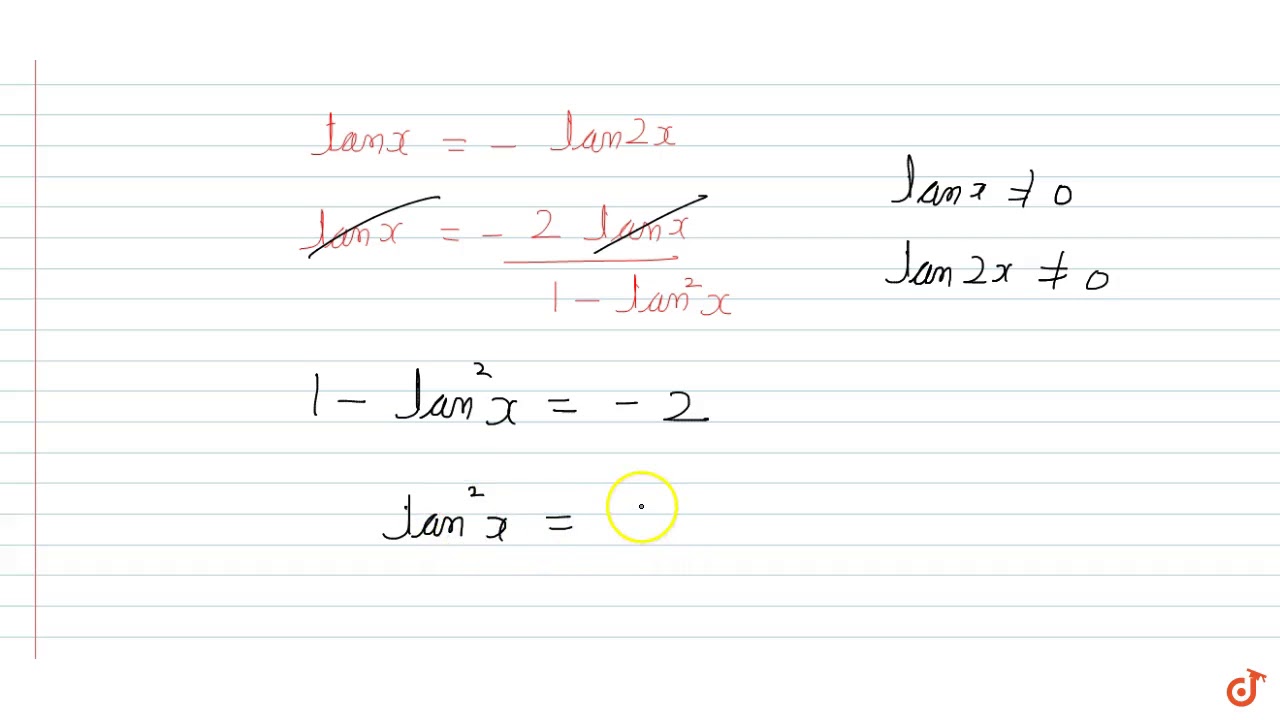



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube
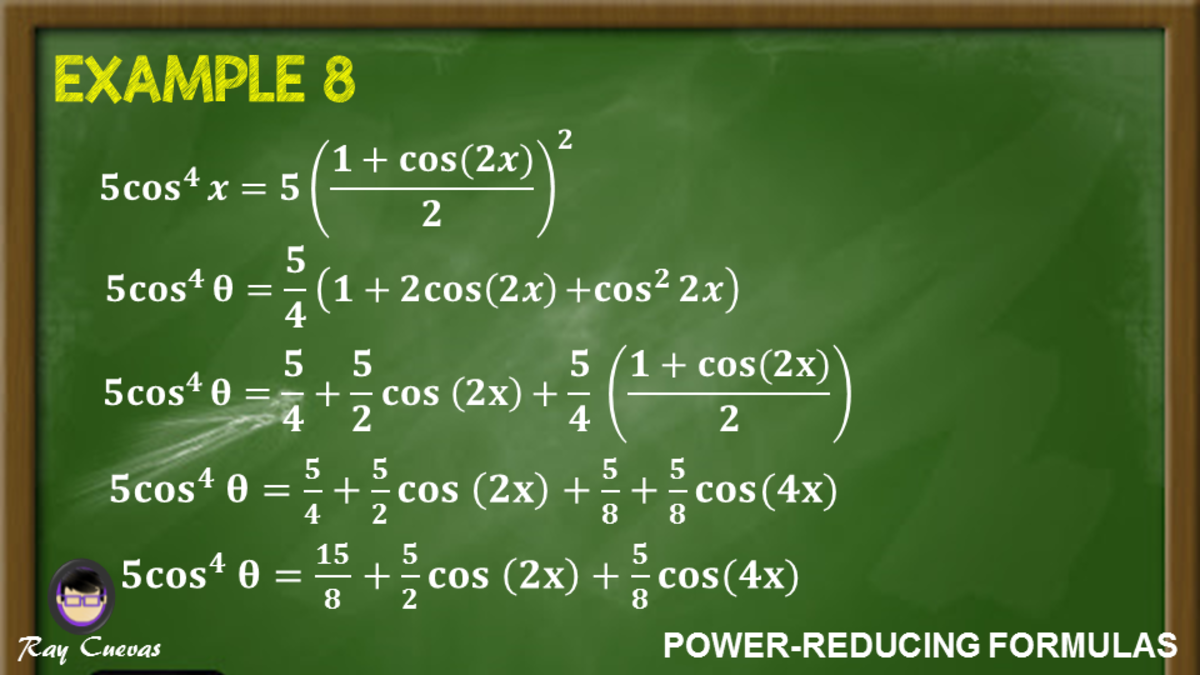



Power Reducing Formulas And How To Use Them With Examples Owlcation
Solve the equation tan( 2 x) = 1 tan( x) ( x) I have tried putting u = t a n ( x), and t a n ( 2 x) = 2 u 1 − u 2 so that − u 3 u 2 3 u = 1, but I can't find any roots that would help me I have also tried using all the trigonometric identities I could think of but that hasn't helped me either, so I have a feeling that I shouldFor the tan function, the equation is tan θ 2 = ± 1 − cos θ 1 cos θ {\displaystyle \tan {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1\cos \theta }{1\cos \theta }}}} Then multiplying the numerator and denominator inside the square root by (1 cos θ) and using Pythagorean identities leads toLearn formula of tan(2x) or tan(2A) or tan(2θ) or tan(2α) identity with introduction and geometric proof to expand or simplify tan of double angle




Cos 2x




Trigonometric Identities Trigonometric Functions Trigonometry
Trig Formulas 2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x Geometry Fomulas Area of a Square A s2 1 Area of a Triangle Abh 2 Area of an There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² A3 The formula cos2A = cos2 A−sin2 A We now examine this formula more closely We know from an important trigonometric identity that cos2 Asin2 A = 1 so that by rearrangement sin2 A = 1− cos2 A So using this result we can replace the term sin2 A in the double angle formula This gives




Limit X Tends 0 X 2 Tan2x Tanx Brainly In



2
Free online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display adsTrigonometric Simplification Calculator \square!Double angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 x




Challenge Trigonometric Equation Tan2x 8 Cos 2x Cot X Youtube
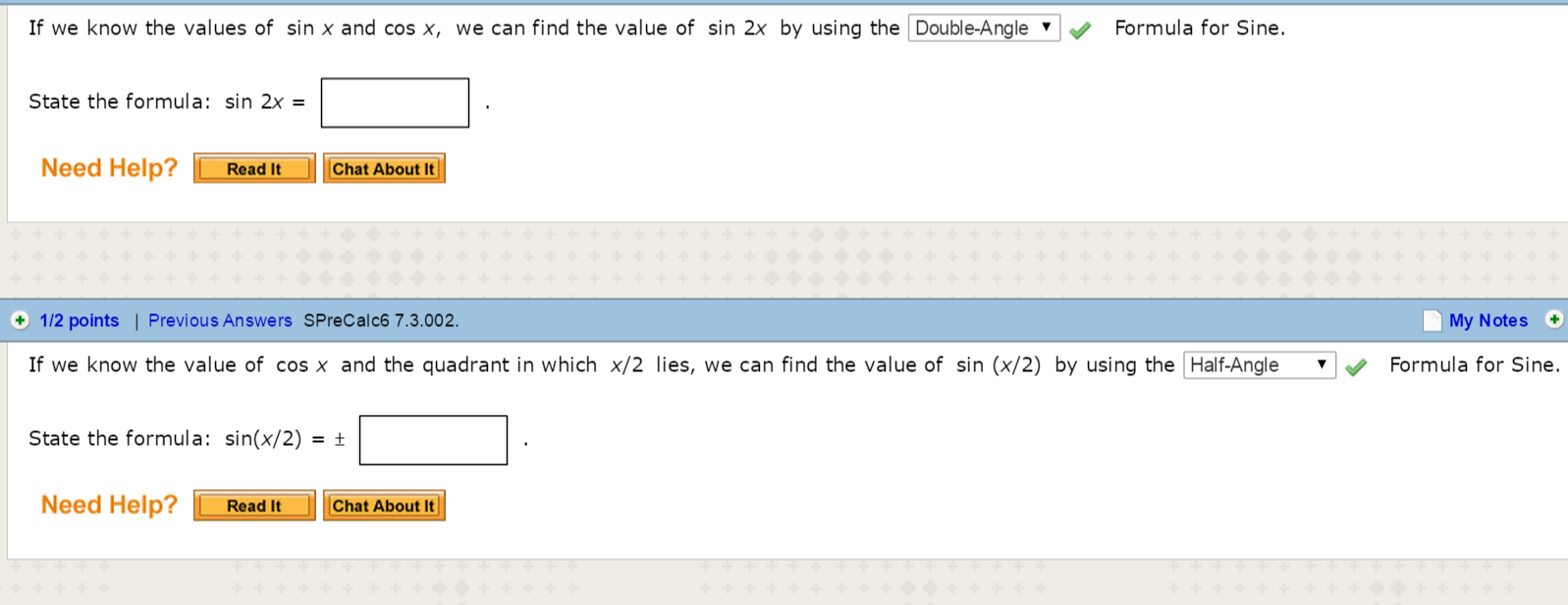



Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
Trigonometric derivatives There are six basic trig functions, and we should know the derivative of each one When we differentiate a trig function, we always have to apply chain rule For instance, in y = sin x y=\sin {x} y = sin x, the sin \sin sin and x x x are not multiplied together Instead, the x x x is the argument of the sine functionJanuary 10 8 Solve cosec2 2x – cot 2x = 1 for 0 x 180 (7) June 10 1 (a) Show that 1 cos2 sin2 = tan θ (2) (b) Hence find, for –180° ≤ θ < 180°, all the solutions of 1 cos2 2sin2 = 1 Give your answers to 1 decimal place (3) January 11First of all, you have to be confident with the identity tan (AB) = (tanAtanB)/ (1tanA•tanB)eq (1) After knowing that you can easily calculate what is tan2A by just modifying the identity as tan2A = tan (AA)= (2tanA)/ (1tan²A)eq (2) After that you can easily solve for tan3A by use same method that is tan3A=tan (2AA)




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples
For the question, tan(2x)tanx = 1, I divided it by tanx, and got the solution as (2n 1) π 6 tan2x = cotx = tan(π 2 − x) So, 2x = nπ π 2 − x So, 3x = (2n 1) π 2 The formula given in my book does not seem to work in Mathcad Prime 30 In the book there is no multiplier (*) printed after tan^2 and cos^2 There is just empty space I did change the formula around in all kinds of ways I put tan inside parenthesis like (tan)^2, or (tan^2* (gammaQ)), or (tan (gammaQ)^2) but nothing worksTan(xy) = (tan x tan y)/ (1−tan x •tan y) sin(x–y) = sin(x)cos(y)–cos(x)sin(y) cos(x–y) = cos(x)cos(y) sin(x)sin(y) tan(x−y) = (tan x–tan y)/ (1tan x • tan y) Double Angle Identities sin(2x) = 2sin(x) • cos(x) = 2tan x/(1tan 2 x) cos(2x) = cos 2 (x)–sin 2 (x) = (1tan 2 x)/(1tan 2 x)




Ppt 5 5 Multiple Angle And Product Sum Formulas Powerpoint Presentation Id




Differentiate The Following From First Principle Tan 2x
Tan ( 2 x) = cos ( x) sin ( x) Convert from cos ( x) sin ( x) to cot ( x) tan ( 2 x) = cot ( x) tan(2x) = cot(x) Move all terms containing x to the left side of the equation Tap for more steps Subtract cot ( x) from both sides of the equation tan ( 2 x) cot ( x) = 0 Simplify each term Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin andTrigonometry Formulas for class 11 (PDF download) Trigonometry is quite a interesting subject Here are the useful Trigonometry Formulas for class 11 Maths Basic Formula tan(x) = sin(x) cos(x) t a n ( x) = s i n ( x) c o s ( x) cot(x) = cos(x) sin(x) c o t ( x) = c o s ( x) s i n ( x) Reciprocal Identities cosec(x) = 1 sin(x) c o s e c ( x
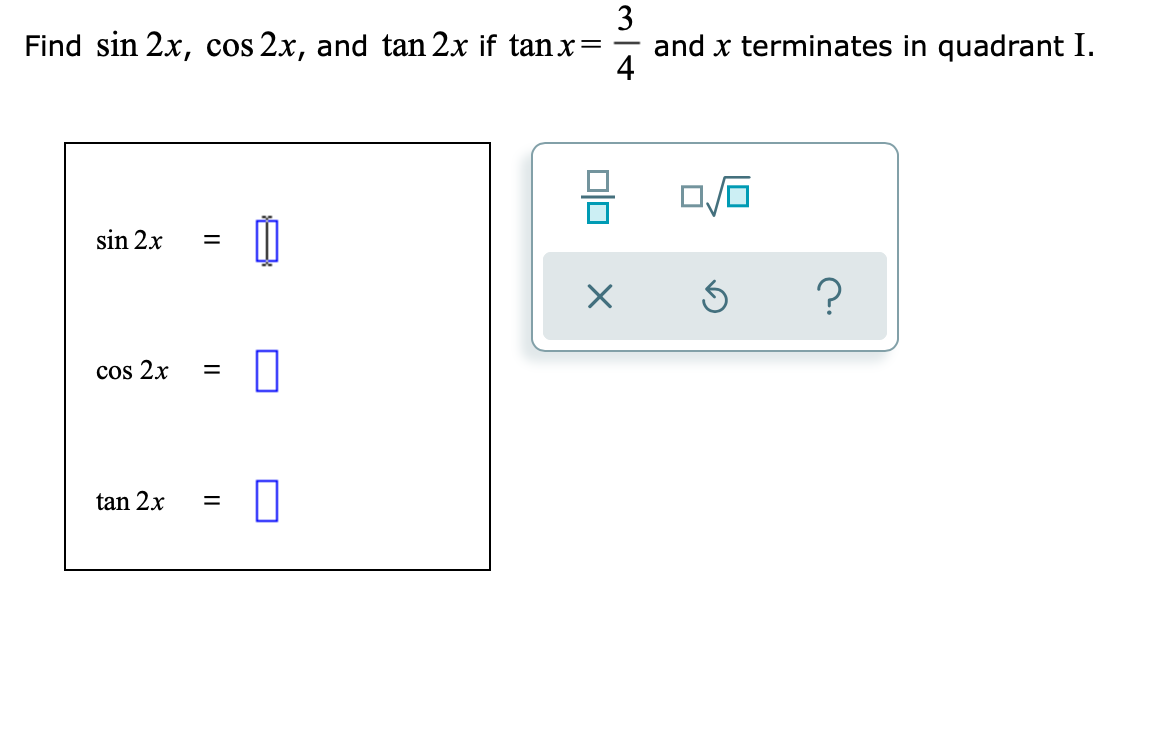



Answered 3 And X Terminates In Quadrant I 4 Bartleby




Prove That Tan 8x Tan 6x Tan 2x Tan 8x Tan 6x Tan 2x
All Trigonometry Formulas List Most Trigonometry formulas revolve around ratios and extremely handy to solve complex problems in Trigonometry If you want to appear for any competitive exams after your school then handson knowledge of different Trigonometry formulas is essential The basic of any Trigonometry formula is a Trigonometry IdentityTangent Ratio Definition & Formula The tangent ratio is a tool used with right triangles that allows one to find the length of the sides of a triangle given the degree of its anglesBut this exercise wants the answer "in full generality" Obviously, I can't list out all of the solution values, because there are infinitely many of them So I'll have to use a formula From what I know about the graph of the tangent, I know that the tangent will equal 1 at 45° after every 180°



The General Solution Of The Equation Tanx Tan2x Tan2x Tanx 2 0 Is Youtube




Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Ex dx = ex C ax dx = ax lna C 1 x dx =lnx C cosxdx=sinxC sec2 xdx=tanxC sinxdx= −cosx C csc2 xdx= −cotx C secxtanxdx=secx C 1 1x2 dx =arctanxC 1 √ 1− x2 dx =arcsinxC cscxcotxdx= −cscx C secxdx=lnsecxtanx C cscxdx= −lncscxcotx C xn dx = xn1 n1 C, when n = −1 Here areShop the official Clinique website for skin care, makeup, fragrances and gifts Read reviews & get Free Shipping today Allergy Tested 100% Fragrance Free



2



Solved Givencos 3 0 5 Findtan2 6 Use The Formulatan2x 1 Cos2x 1 Cos2x Course Hero
Precalculus Trigonometric Functions A trigonometric equation is any equation that includes a trigonometric function There are two basic types of trigonometric equations identities and conditional equations Identities are equations that hold for any angle Conditional equations are equations that are solved only by certain anglesCreate your account The derivative of tan 1 is 2 14x2 2 1 4 x 2 Finding the derivative of Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer link



Q Tbn And9gctufmrsc12qufe Whtfdvvuwzj Z1m2v6 P T5bb9h Rcw17hdb Usqp Cau




Sin2x Cos2x 1 Proof
The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is Where x is the angle




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Class 12 Maths Formula For Chapter 2 Inverse Trigonometric Functions



Http Ougouag Com Trigreviewforcalc Pdf




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Solve Tan X Tan 2x Sqrt 3 Tan X Tan 2x Sqrt 3




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau




The General Solution Of The Equation Tanx Tan2x Tanx Tan2x 1 Is Youtube




The Number Of Solution Of The Equation Tan3x Tan2x Tan3x Tan2x 1 In 0 2pi Is




Verify The Following Equation Show Work On The Pa Gauthmath




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



Http Www Math Brown Edu Tomg Formulas Pdf




Sinx 1 4 X In Quadrant Ii Find The Value Of Sinx 2




Packet 21 Trigonometric Identities Ppt Download




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes
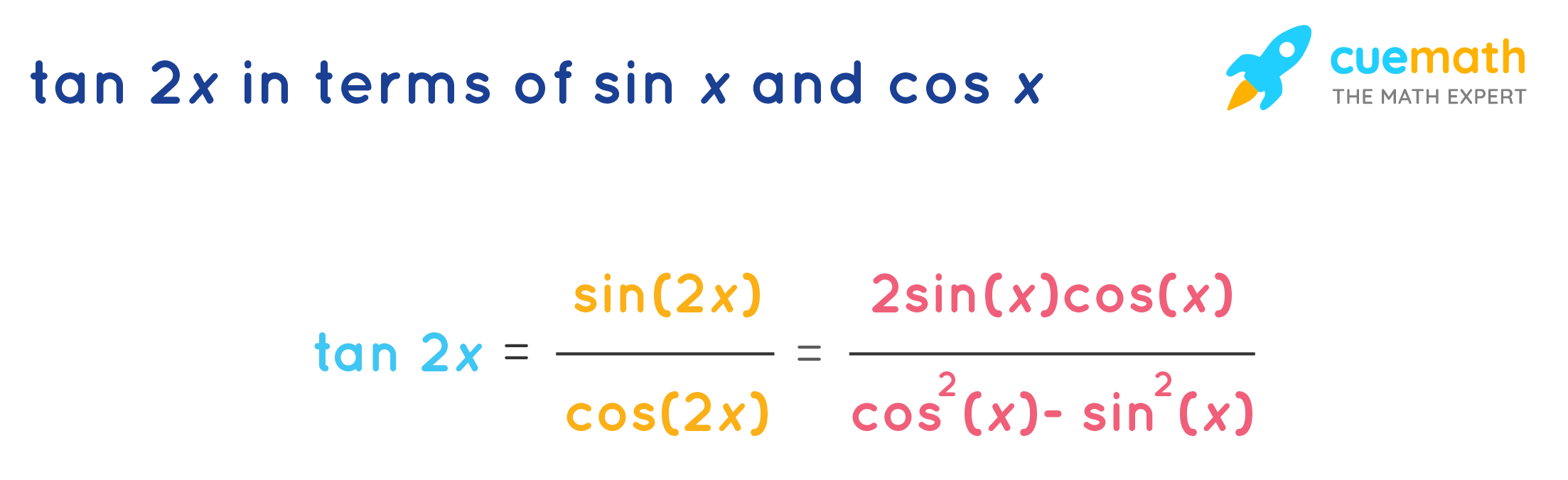



Tan 2x Formula What Is Tan 2x Formula Examples



Tan 2x Tan 2x
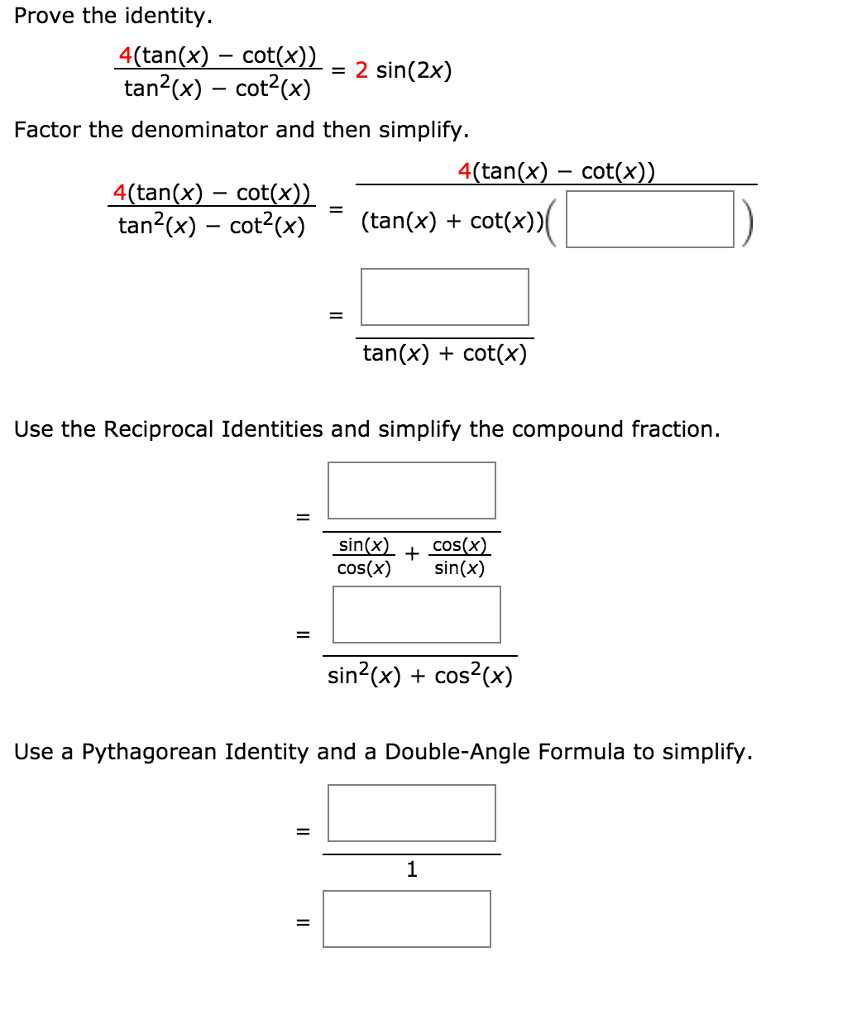



Prove The Identity 4 Tan X Cot X Tan 2 X Chegg Com
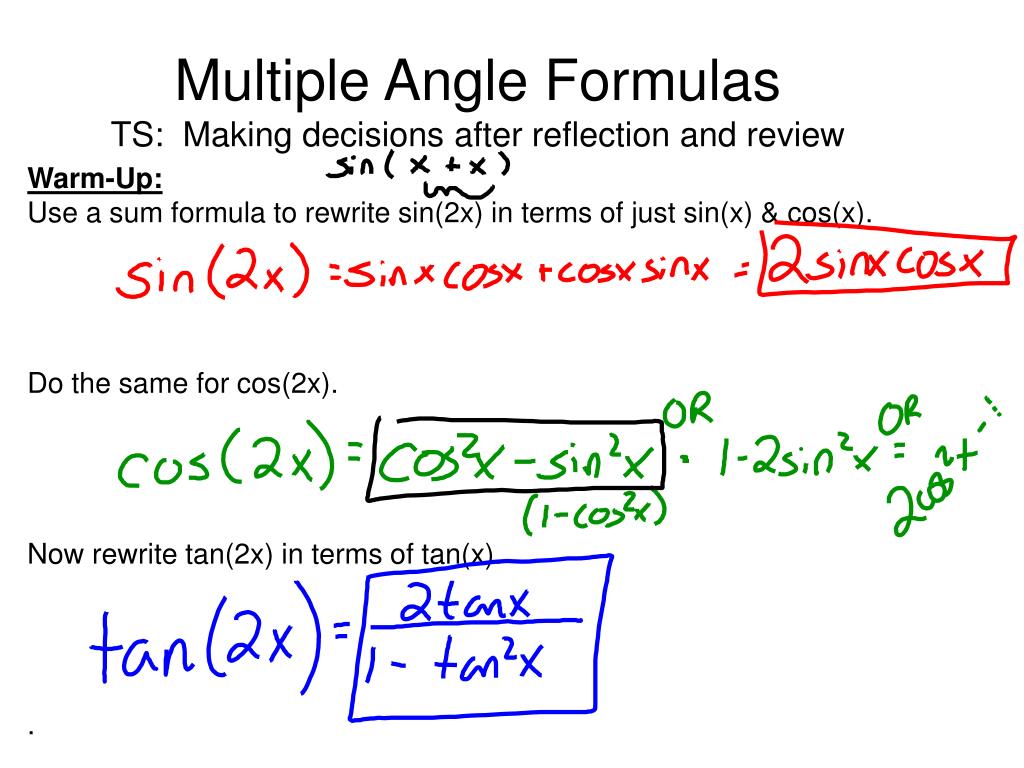



Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id
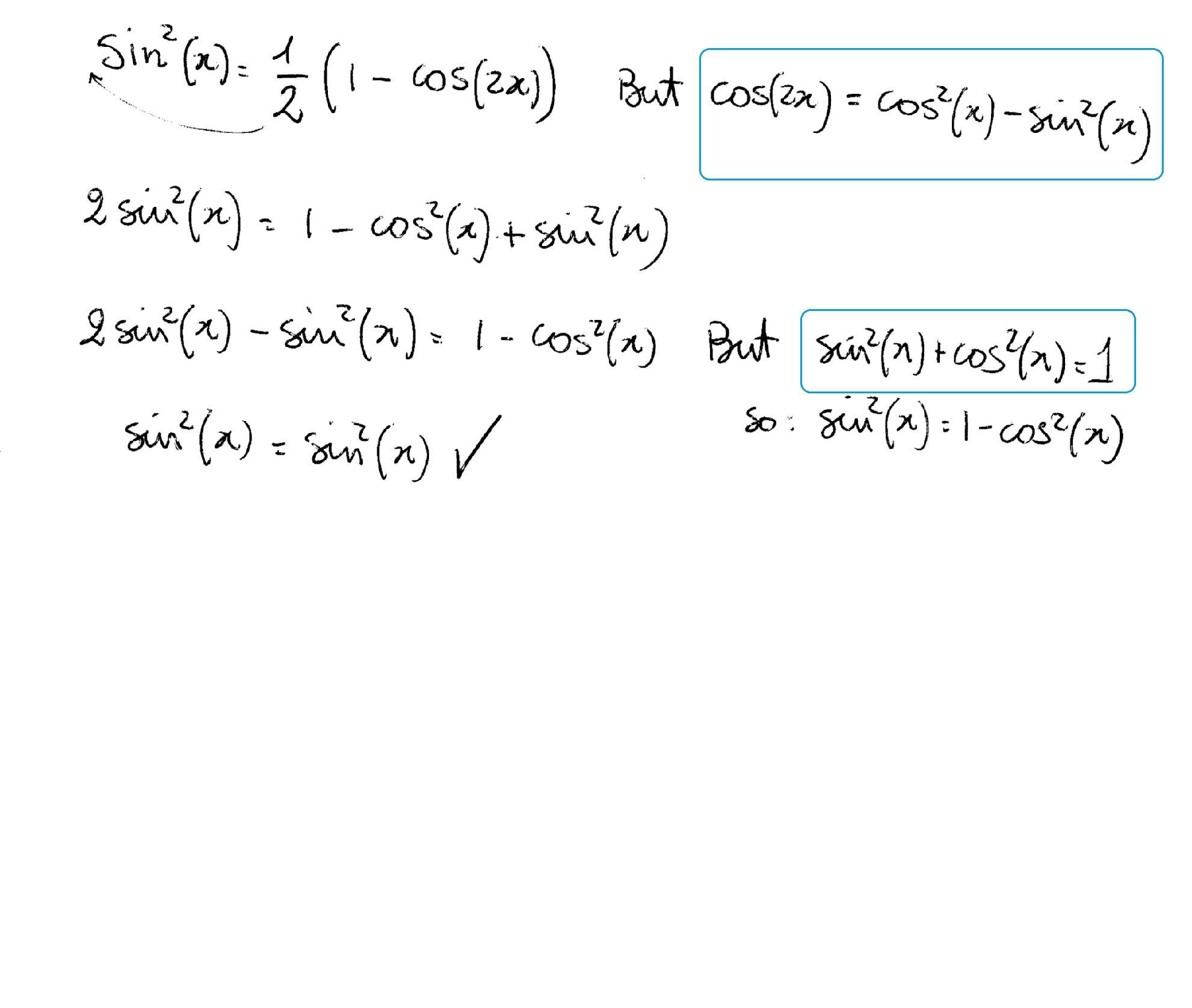



How Do You Verify Sin 2 X 1 2 1 Cos2x Socratic




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3




1 Sin 2 X Formula Sepertikisahku




Lesson 4 5 Double Angle Formulas




Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath
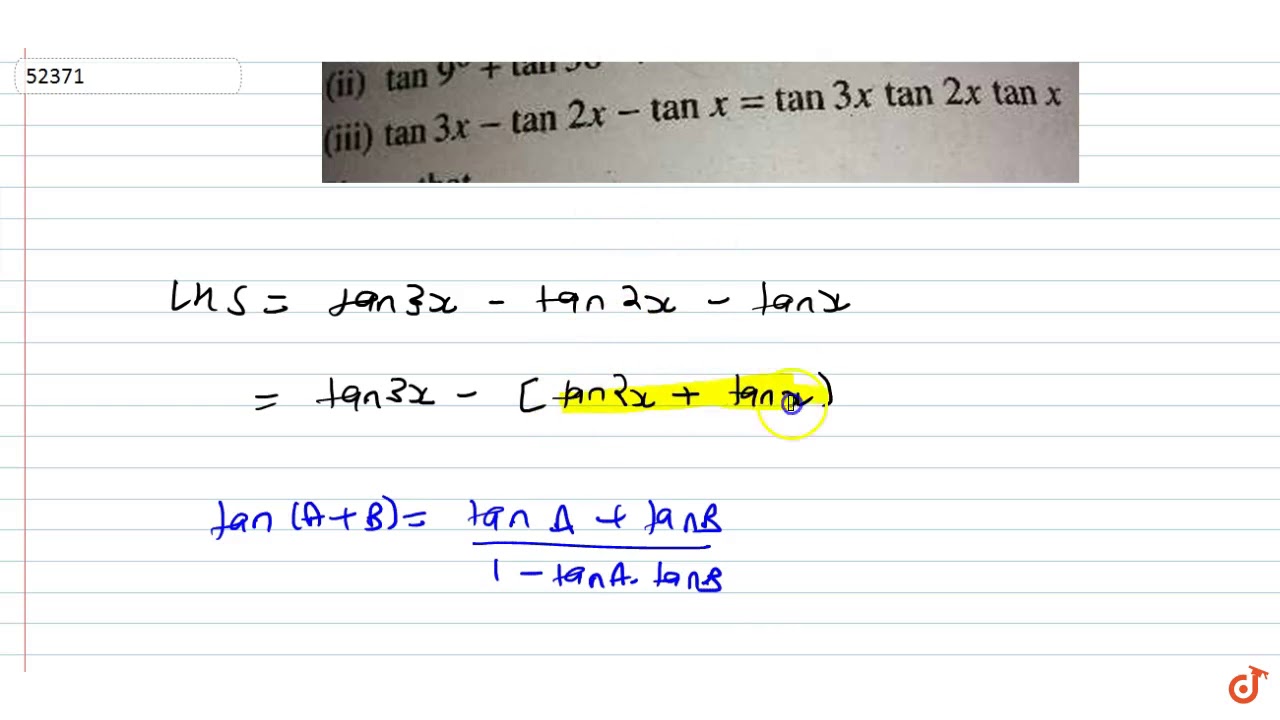



Tan 3x Tan 2x Tan X Tan 3x Tan 2x Tan X Youtube




Sin2x Cos2x 1 Proof




Tanx Tan2x Tan3x 0




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



Solved Dy Suppose 4 Sec2 2x Tan 2x Y 0 4 And Y 0 1 Da 2 A Find A Formula For Y A B Find A Formula For Y A Show And Explain Y Course Hero




Tan 2x Formula What Is Tan 2x Formula Examples
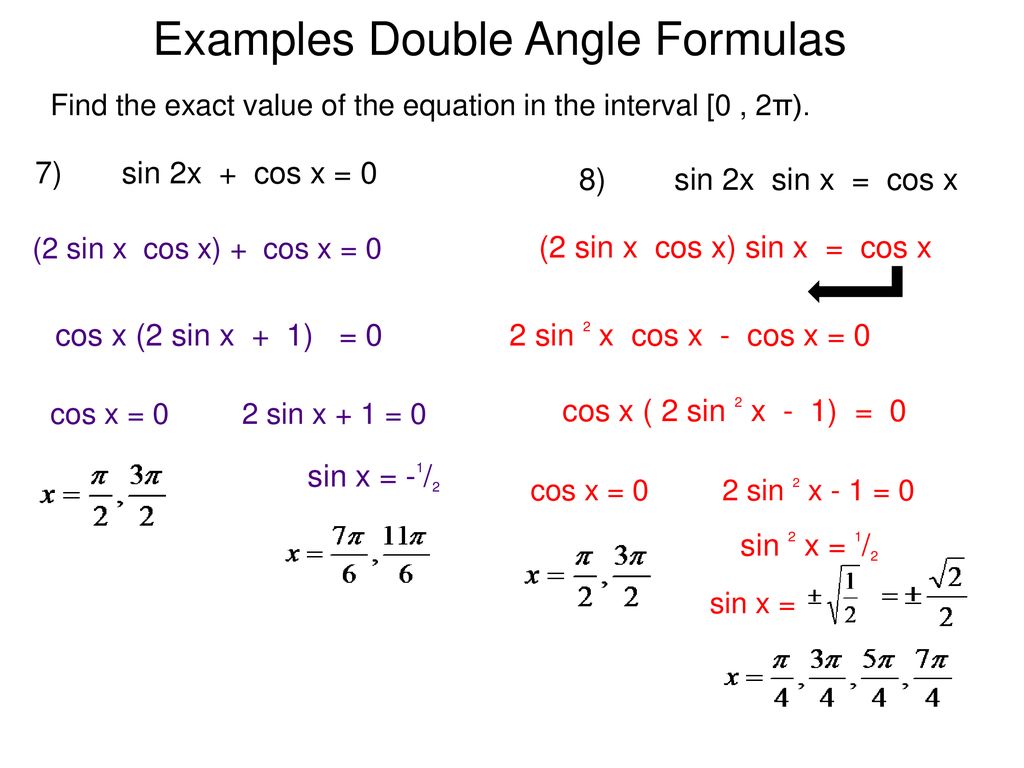



Examples Double Angle Formulas Ppt Download



2



2
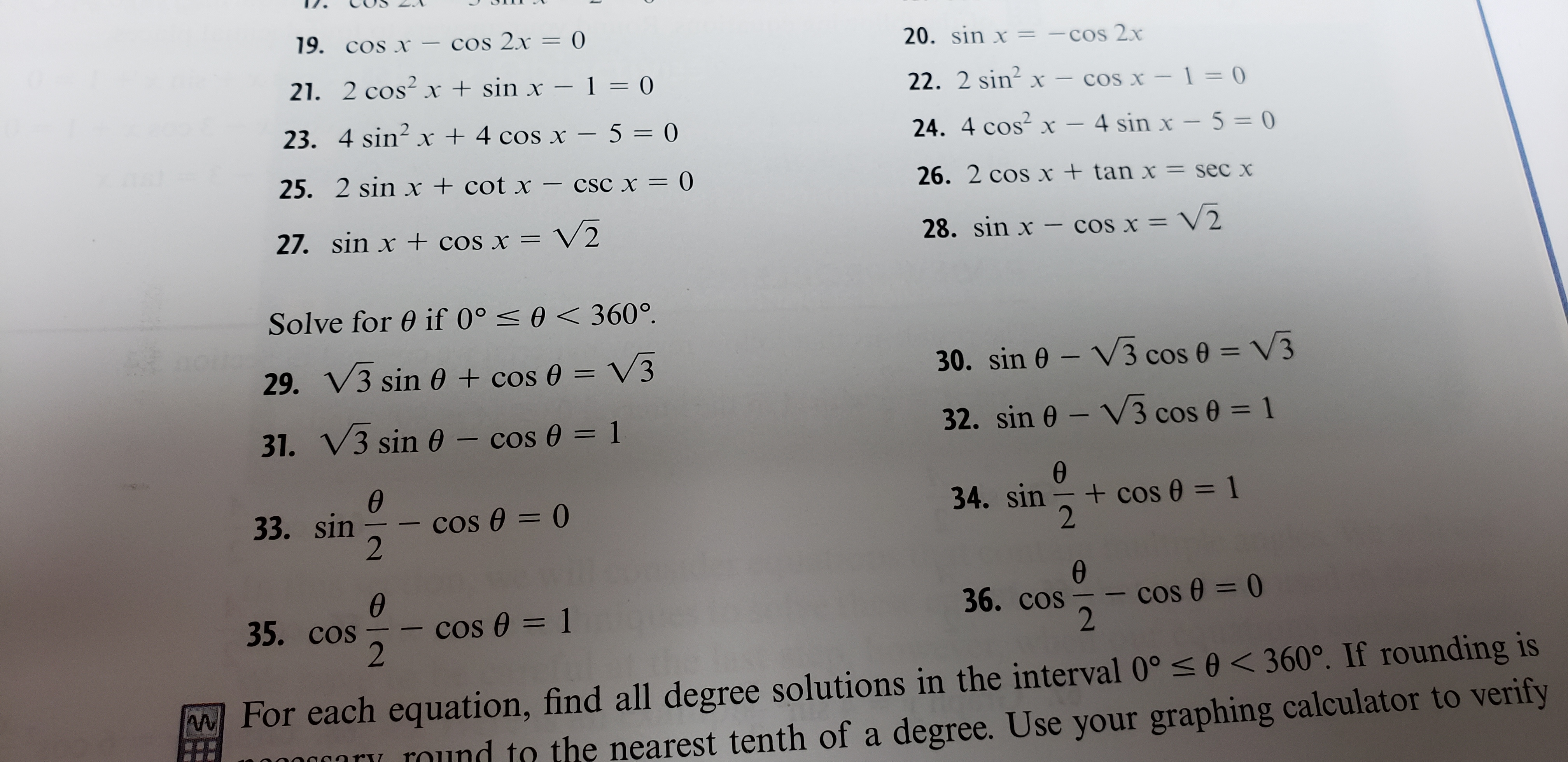



Answered 19 Cos X Cos 2x 0 Sin X Cos 2x Bartleby




Compound Angle Identity Tan 3x Formula Derivation Youtube




How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In




Derivative Rules For Trigonometric Functions




The General Solution Of The Equation Tanx Tan2x Tanx Tan2x 1 Is



Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf




7 Questions On Differential Equations Exam 1 Math 1132 Docsity




Trig Identity Sec2x Minus Tan2x T10 Youtube
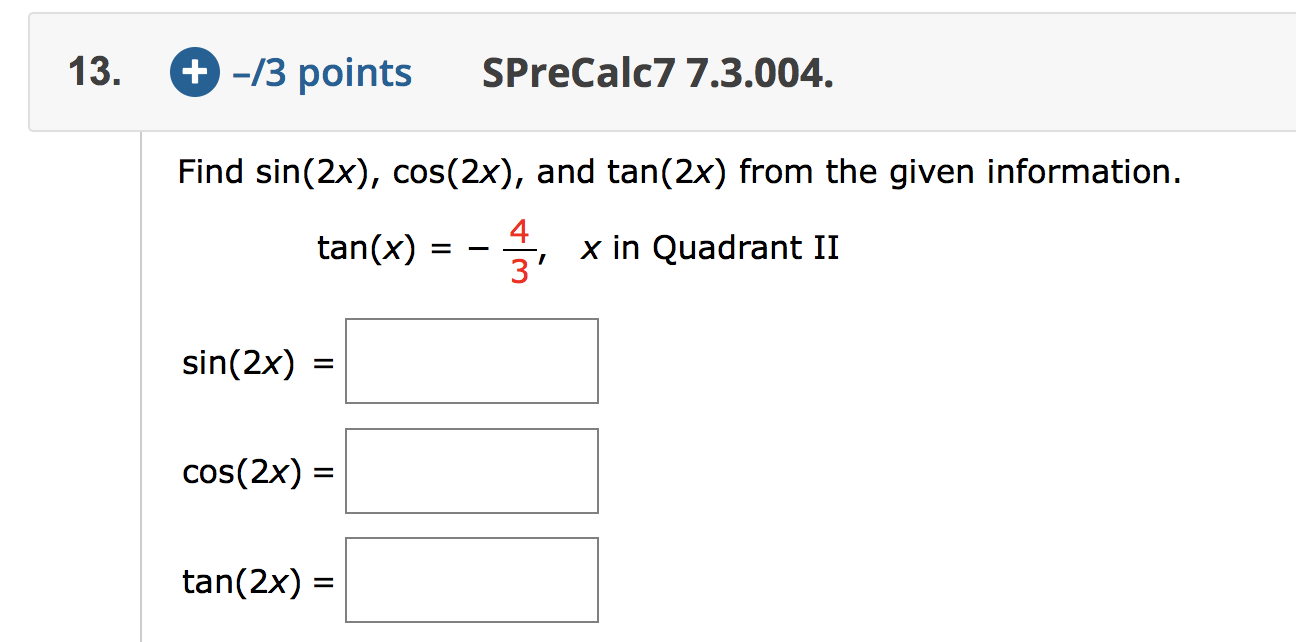



2 Points Sprecalc7 7 3 029 16 Simplify The Chegg Com




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 11 Trigonometric Equations Download Free Pdf




Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com




Cos 2x




Section 7 3 Double Angle Half Angle And Chegg Com
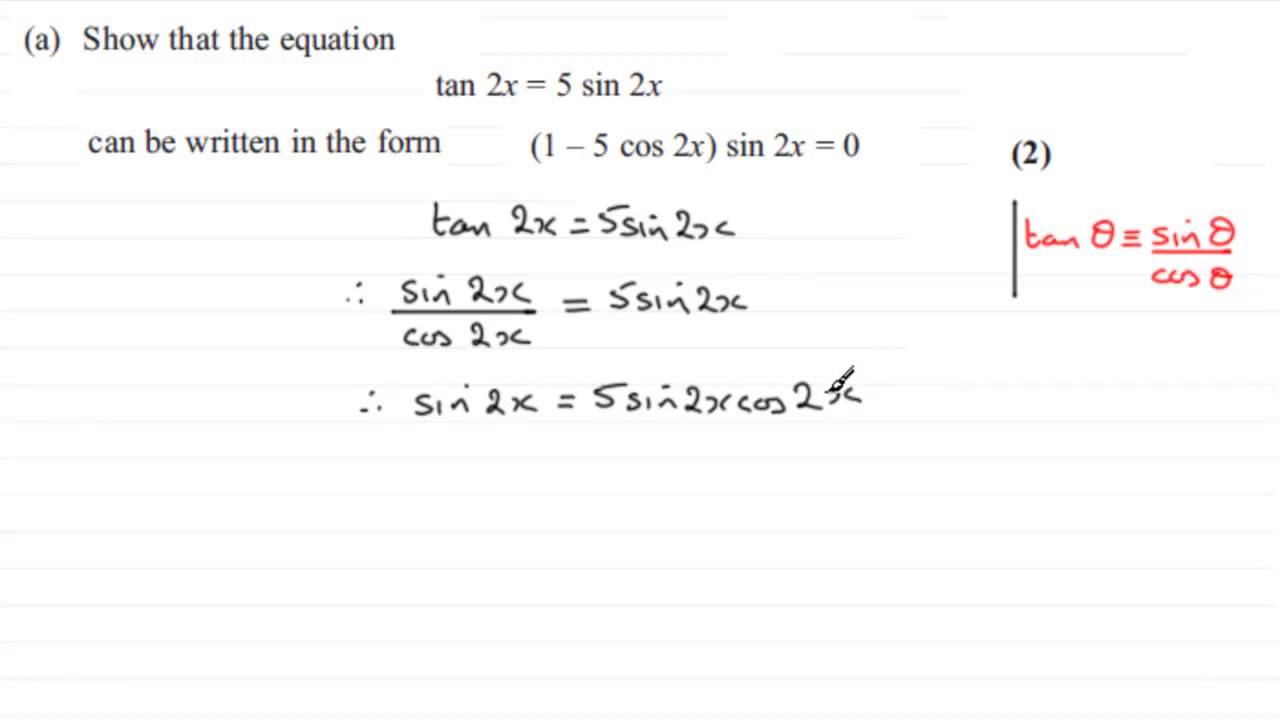



Edexcel Core Mathematics C2 June 12 Solutions Examples Worksheets Videos Activities




Section 7 3 Double Angle Half Angle And Sum




Double Angle Formula Sine Cosine And Tangent Owlcation




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11




Hyperbolic Functions Wikipedia



Www Thatonemathguy Com Uploads 7 0 1 3 Precalculus 2nd Edition Part 2 Pdf




Trigonometric Identities Ppt Download




If Tanx Tan 2x 1 Then The Value Of Tan 4x 2 Tan 3x Tan 2x 2 Tanx K 4 Then K Is Equal To
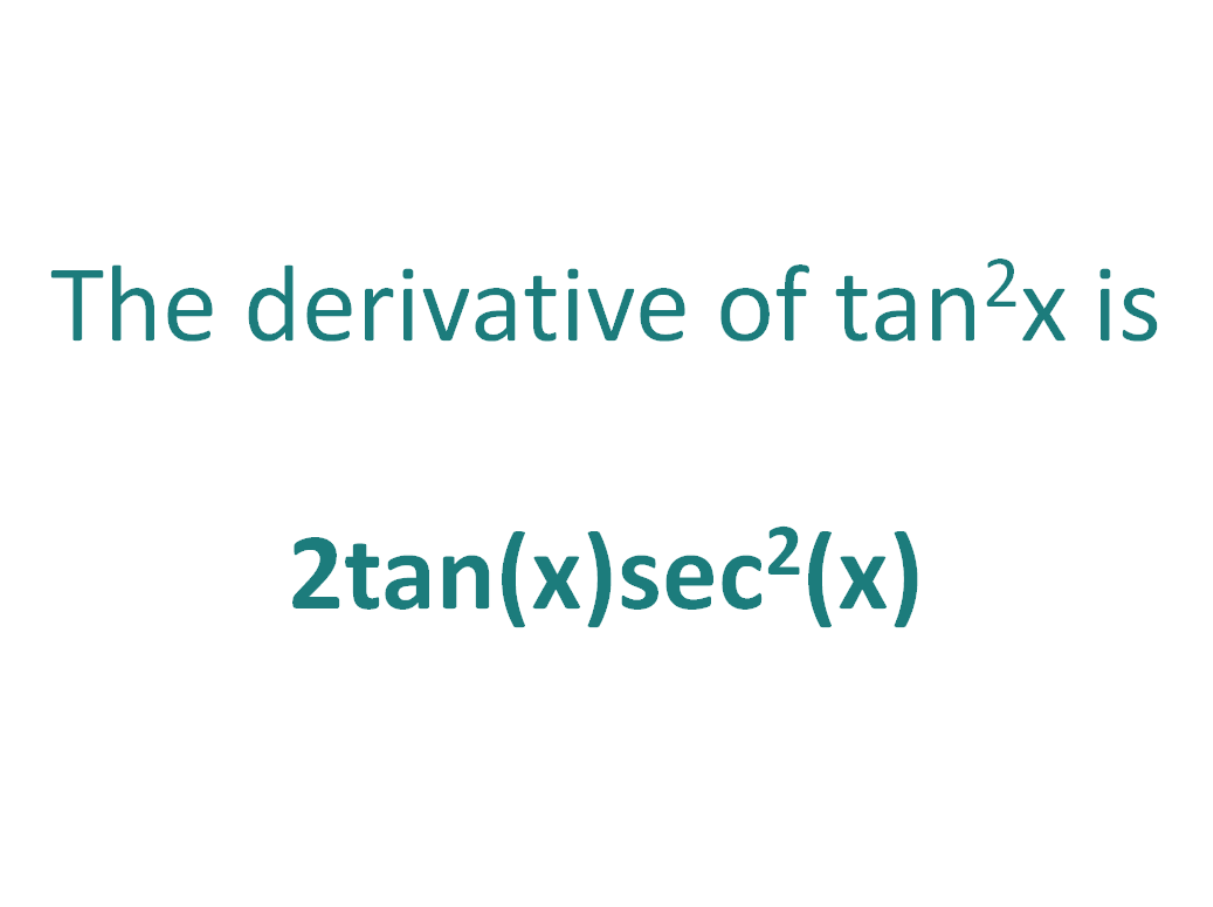



The Derivative Of Tan 2x Derivativeit




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 11 Trigonometric Equations Download Free Pdf



1
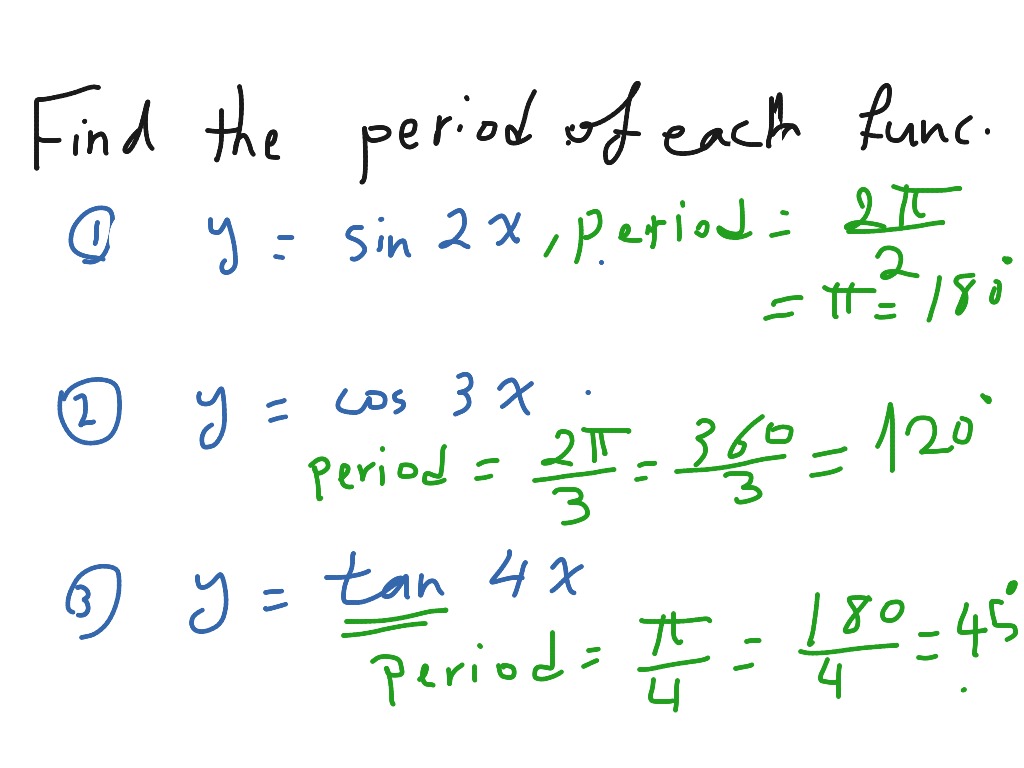



Find The Period Of Sin2x Cos 3x Tan 4 X Math Trigonometry Showme




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians




Examples Double Angle Formulas Ppt Download




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




How Many Can You Derive From First Principles Ppt Download




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1



Www Jensenmath Ca Unit 5 pretest review solutions Pdf




All In One Maths Formula At Your Finger Tips Notes




Find The General Solution For Each Of The Following Equations I Cos 4 X Cos 2x Ii Cos 3x Cos X Cos 2x 0 Iii Sin 2x




1 Point If Sin Va Vb Then By Using A Chegg Com




General Solution Of Tan 2x 3 Sqrt 3 Is




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples




Powers Of Trigonometric Functions




If Sin X 1 5 And X Is In Quadrant I Find The Exact Values Of The Expressions Without Solving For X Wyzant Ask An Expert




Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P 4




Inverse Trigonometric Functions General Solution Of Trigonometric Equations Pdf Dwrean Lhpsh



Q Tbn And9gcr2jamezvnschsup9wyxdzj0wc0knie4dqfphj6okqiboct8vn1 Usqp Cau




Trigonometry Identities And Equations Ppt Download



0 件のコメント:
コメントを投稿