0 ·exp(a·(x−x 0)) 38 Kapitel 8 Potenzreihen und elementare Funktionen Eigenschaften der Exponentialfunktion FunktionalgleichungEs gilt exp(zw)=exp(z) ·exp(w) f¨ur alle z,w∈C Folgerung F¨ur die Exponentialfunktion gilt (a) exp(z) =0f¨ur alle z∈C;Hinweis für Programmierer Um die Umkehrfunktion zu bestimmen, kann man für jeden yWert die Nullstelle der Hilfsfunktion h(x) = x·e x y berechnen Für y > 0 ist das Newtonverfahren das geeignete, für y kleiner 0 nicht, da die Funktion h bei 1 eine waagrechte Tangente hat Mit dem Intervallhalbierungsverfahren ist die Ermittlung der Nullstelle von h jedoch kein ProblemDie Formel (5) trifit zu f˜ur x= 0 Ist (5) f˜ur ein beliebiges x2Zrichtig, so gilt auf Grund von (2) und der Regeln ˜ub ers Potenzrechnen erstens exp(x 1) = expx¢exp1 = ex¢e= ex1 und zweitens exp(x¡1) = expx=exp1 = ex=e= ex¡1 Somit trifit (5) f˜ur alle ganzzahligen xzu Ist nun weiter x= p=qmit p2Z, q2N⁄, so gilt nach dem schon

Elements Of Analysis
Integral exp(-x) from 0 to infinity
Integral exp(-x) from 0 to infinity-(b) exp(−z)=1/exp(z) f¨ur alle z∈C;76 KAPITEL 5 DIFFERENZIERBARE FUNKTIONEN 5 f(x) = exp(λx),λ∈R exp0(λx) = lim h→0 exp(λ(xh))−exp(λx)h = lim h→0 exp(λx)·(exp(λh)−1)h = exp(λx



Home Hvl No Ansatte Tct Ftp V hydrodynamikk Matlab Ch03ny Eksempler Pdf
Integral of exp(x^2)Instructor Christine BreinerView the complete course http//ocwmitedu/1802SCF10License Creative Commons BYNCSAMore information aFur˜ x 2 R deflnierte Funktion exp R ! Aufgabe Wie kann ich zeigen, dass für x > 0 gilt ex = exp(x) Problem/Ansatz Ich weiß es ist das gleiche, aber wie zeigt man das?
2 1 0 1 2 x f(x) exp (x) 1 x 1 0 1 3 5 7 x f(x) log (1 x) x Wir appro ximieren exp (x) an der Stelle 0 durch eine Ger ade exp (x) = 1 x Wir appro ximieren log (1 x) an der Stelle 0 durch eine Ger ade log (1 x) = x Josef Le ydold c 06 Mathematische Methoden IX Taylorreihen 9 / 25= 1 x 1 2 x2 1 6 x3 1 24 x4 1 5! Angenommen es gäbe nun ein x mit exp(x)=0 Dann würde gelten > exp(0)=exp(xx)=exp(x)*exp(x)=0 Und da haben wir den Widerspruch Es wäre dann sogar exp(y) = 0 für alle y aus C, denn exp(y) = exp(yxx) = exp(yx)*exp(x) = exp(yx)*0 Also Wenn die Exponentialfunktion an irgendeiner Stelle ungleich 0 ist, dann muss sie überall ungleich 0 sein
Und woher kommt eigenlich exp(x)??Y = ln(x) x = exp(y) exp0(y) = exp(y) = x ln0(x) =1=x 1 x 1 x ln0(x) = 1 x Logarithmen zur Basis 2 Wir erinnern uns Der nat urliche Logarithmuslnx ist die Umkehrfunktion der eFunktion ex Die Funktionlog2 x, der Logarithmus zur Basis 2, ist analog de niert als die Umkehrfunktion von2x Also b = log2 a , a = 2b oder auch a = 2log2 a Aus a = 2log2 a folgt durch Logarithmierenlna = log2 I strongly suggest to first get a "feeling" for the graph 0) 2) sin(x) ≈ x (x much smaller than π/2) 3) ex goes monotoinc to zero (∀ x ∈ R, x ≥ 0) 4) ex has sample values at e 0 = 1, eπ ≈ , e2⋅π ≈ , e3⋅π ≈ , e4⋅π ≈ , From this, you can postulate that the roots for ex sin(x) are ≈ 059 (for the root between 0 and π




Exponential Family Distribution And Sufficient Statistic Mathematics Stack Exchange



Www Jstor Org Stable
Exp(z)= X∞ k=0 1 k!The property exp(x)0 = exp(x)is the core ofdefinition (D5) It is this property that makes the exponential function important for calculus It is also the reason why students like to differentiate the exponential function Although the definition implicitly contains a differential equation and thus seems to be a highly advanced definition, it could be explained to students as soon asExp(x) = X1 n=0 xn n!



Www Somervillenjk12 Org Cms Lib5 Nj Centricity Domain 80 Ws 8 4 eulers method answers Pdf



Euler S Equation
Beweis Indemwirableitenergibtsich d dt exp(tA) X 0 Zt 0 exp(−sA)G(s)ds = Aexp(tA) X 0 Zt 0 exp(−sA)G(s)ds exp(tA) d dt Zt 0 exp(−sA)G(s)ds = Aexp(tA) X 0 Zt 0 exp(−sA)G(s)ds G(t) = AX(t)G(t) Sei Y(t) eine weitere Lösung des Anfangswertproblems Y0 = AY, Y(0) = X 0 Wir betrachtenZ(t) = X(t)−Y(t) Ableitenergibt Z 0= X RE exp(x)?0 Aus der Definition von (welche ihr auch genommen habt) sollte leicht zu sehen sein, dass für alle Zusammen mit kann man nun folgern, dass es auch für alle gilt , 1527 METHMETH Auf diesen Beitrag antworten » RE exp(x)?0 Laut Definition gilt doch bereits für jedes x Element der Reellen Zahlen, dass exp(x)>0 ist`lim_(x>oo)exp(x)=0` The exponential function has a limit in `oo` which is `oo` `lim_(x>oo)exp(x)=oo` Equation with exponential ;




Taylor S Theorem Wikipedia
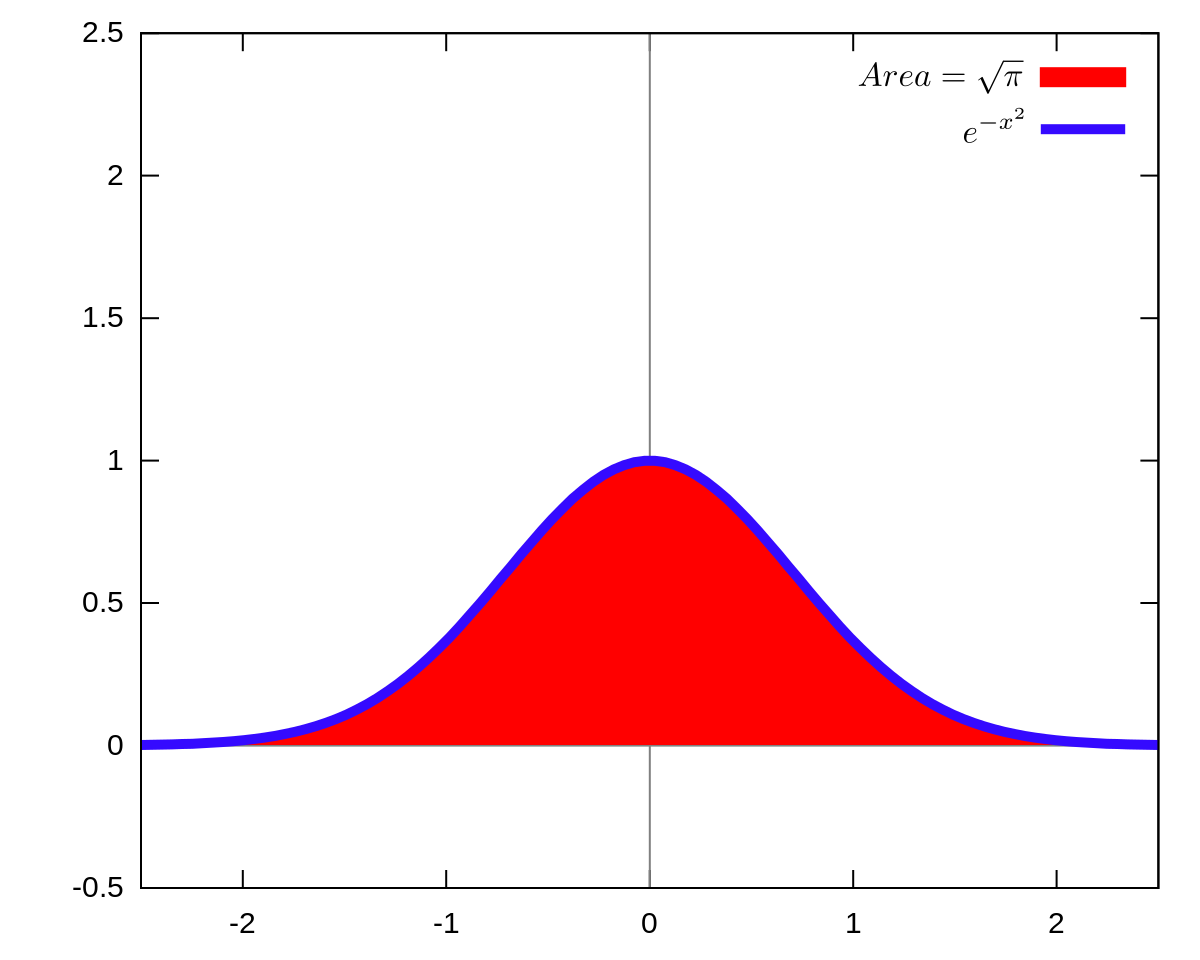



Gaussian Integral Wikipedia
Exp(0) = 1 Bemerkung Es folgt, dass g(x) = aexp(bx)die Gleichungen g0(x) = bg(x)und g(0) = a Die Exponentialfunktion benutzt man deswegen, um Prozesse mit der Eigenschaft Wachstumsgeschwindigkeit proportional zur erreichten Gr oˇe zu modellieren Beispiele unbegrenztes Wachstum einer Population (Bakterienkolonie) Moore'sches Gesetz (su) Wie kann man exp(xF¨ur x < 0 ist F(x) = 0, und f¨ur x > 1 gilt F(x) = 1, also F(x) = x ∧1 (Gleichverteilung) Insbesondere ist F absolutstetig mit Dichte f(x) = F′(x) = 1 0,1(x) fur fast alle¨ x (3) (ii) F¨ur x ≤ 0 gilt F(x) = P(−T ≤ x) = P(T ≥ −x) = ex (4) F¨ur x > 0 ist F(x) = 1, also F(x) = exp(x) ∧1 Insbesondere ist F absolutstetig mit Dichte f(x) = ex1 (−∞,0)(x) f¨u (5) 2Tabelle einfacher Ableitungs und Stammfunktionen (Grundintegrale) Diese Tabelle ist zweispaltig aufgebaut In der linken Spalte steht eine Funktion, in der rechten Spalte eine Stammfunktion dieser Funktion Die Funktion in der linken Spalte ist somit die Ableitung der Funktion in der rechten Spalte Hinweise Wenn




In The Taylor Series Expansion Of X Sin X About The Point X Pi The Coefficient Of X Pi 2 Is




The Function F X E X Is A Continuous Everywhere But Not Differentiable At X 0 B Continuous And Differentiable Everywhere C Not Continuous At X 0 D None Of The Above
R heit Exponentialfunktion Man setzt X1 n=0 1 n!Stetigkeit der Exponentialfunktion Satz Die Funktion exp(x) ist stetigBeweis Nach Satz 610 gilt exp(x)∑N n=0 xn n!= exp(1) = e (Eulersche Zahl) Sp˜ater werden wir exp(x) = ex schreiben, aber zuvor mu gezeigt werden, da in der Tat exp(n) = en f˜ur n 2 Z gilt Will man exp(x) n˜aherungsw eise aus der Exponentialreihe berechnen, so mu man eine " Fehlerabsch˜atzung \ haben (9




The Value Of The Integral Overset 1 Underset 0 Int E X 2 Dx Lies In The Integral




Misc 40 Evaluate 0 1 E2 3x Dx As A Limit Of A Sum Miscellaneous
K=0 a ksin(exp(x k1)) auf punktweise und gleichm aˇige Konvergenz auf R; Also gilt \(\exp(t)=x(t)>0\) Beantwortet von LC 1,7 k Hallo LC, danke für deine Antwort, aber kannst Du mir nochmal etwas ausführlicher (wobei es schon ausführlich genug ist) die einzelnen Rechenschritte erklären mit dem Summenzeichen? Foggyut , 1802 e Funktuionen löst man meist mit einem dekadischen Logarithmus auf In diesem Fall gibt es jedoch keine Lösung Ansatz xe^x=0 e^x=x ln (e^x)=ln (x) Die Logarithmus Funktion hat die einschränkenden Bedingungen x>0 also ist die Gleichung (im relativen Bereich) nicht lösbar 1 Kommentar



Home Hvl No Ansatte Tct Ftp V hydrodynamikk Matlab Ch03ny Eksempler Pdf




Compute The Moment Generating Function Mgf Of X Chegg Com
In Pure and Applied Mathematics, 19 Lemma The exp is d X)YThe eigenvalues of (I – e –ad X)/ad X are the numbers (1 – e μ)/μ with μ of the form σ – γ and σ, γ are eigenvalues of X (here (1 – e z)/z = − 1 if z = 0)Since, (1 – e z)/z = 0 if and only if z = 2πik That is, Similarly, Therefore As for , apply l'Hopital's rule, this limit is equal to Similarly, and therefore the derivative at is zero You should now be able to show that the th derivative at is zero for all Share edited Nov 3 '15 at 127 answered Nov 3 '15 at 031Dieser Artikel steht unter einer freien CCBYSA 30 Lizenz Damit kannst du ihn frei verwenden, bearbeiten und weiterverbreiten, solange du „Mathe für NichtFreaks" als Quelle nennst und deine Änderungen am Text unter derselben CCBYSA 30 oder einer dazu kompatiblen Lizenz stellst




Rd Sharma Solutions For Class 11 Chapter 3 Functions




Misc 18 General Solution Ex Dy Y Ex 2x Dx 0 Miscellaneous
Die Exponentialfunktion zur Basis a > 0, \, a \neq 1 a > 0, a =/ 1 ist eine Funktion der Form x \mapsto a^x x ↦ ax1 2 ˙ Wegen g(x;y) = (4x2 y2)exp( x2 4y2) 0 = g(0;0) f ur alle ( x;y) 2R2 ist sofort klar, dass gbei (0;0) ein globales Minimum hat und dieses betr agt 0 Ferner haben wir @2g @x2 (x;y) = ( 224x2 22y2 8)exp( 2x 4y) ( 8x3 2xy2 8x)exp( x2 4y)( 2x) = (16x4 4x2y 2 40x 2y2 8)exp( x2 4y2); exp(x) sinx = 0 Learn more about f(x), math
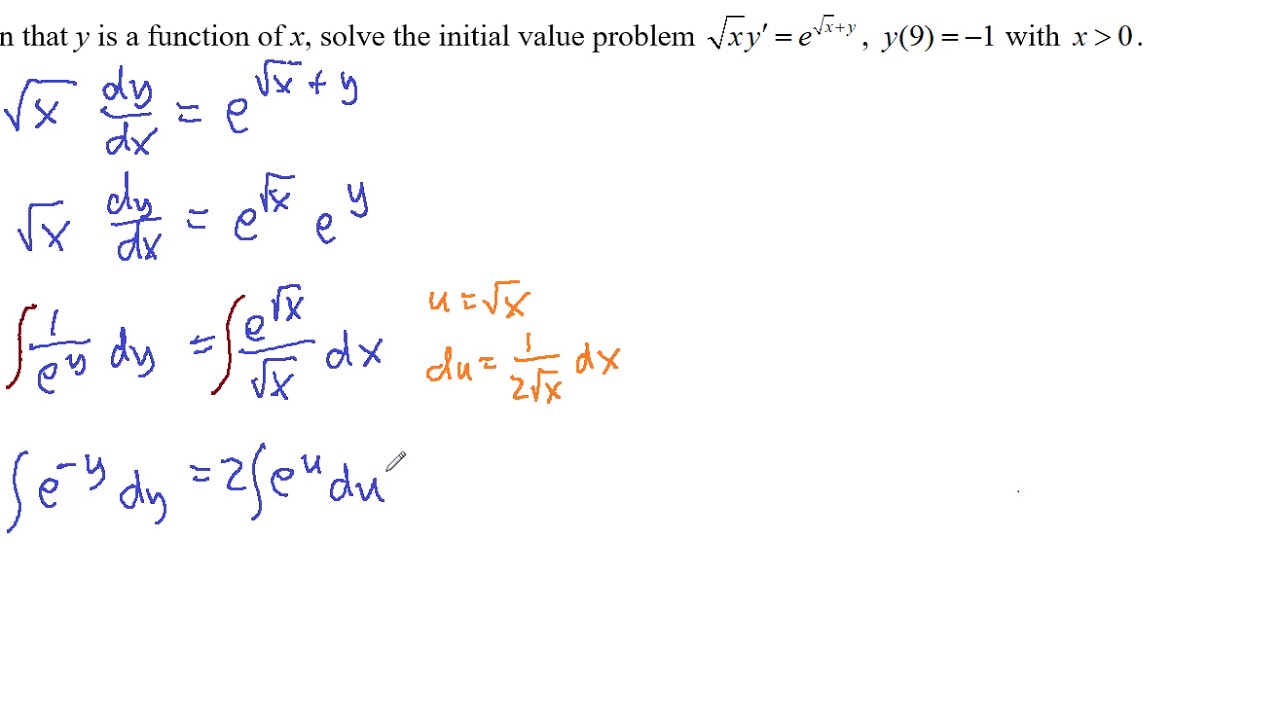



First Order Differential Equations



Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf
Kommentiert von Integraldx Im zweiten Beweis wird zunächst \( \exp(x)\exp(xExp(x) = exp(limrk) = limexp(rk) = limerk=elimk!1rk=exk!1k!1k!1 Somit stimmt die Exponentialfunktion fur reellexmit der aus der SchulebekannteneFunktionuberein Satz Die Exponentialfunktion besitzt inCkeine Nullstellen (Dh, es istexp(z)6= 0 fur allez2C)Exp(X T) = (exp X) T, where X T denotes the transpose of X exp(X ∗) = (exp X) ∗, where X ∗ denotes the conjugate transpose of X If Y is invertible then e YXY −1 = Ye X Y −1 The next key result is this one If = then = The proof of this identity is the same as the standard powerseries argument for the corresponding identity for the exponential of real numbers That is




At What Values Of X Does F X 0 A 4 B 0 C 4 D 2 E 1 F 8 Brainly Com




Problem 1 Solve The Following Quasilinear Pdes 1 Ux Chegg Com
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge6 2 jxjN1 (N 1)!;0(x) = exp(x) ;



What Is The Limit Of E X E X X As X Tends To 0 Quora




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y
Einführung von f(x) = exp(x) Bisher wurde in der Schule die Zahl e als Grenzwert definiert Dazu musste mit viel Vorwissen über Folgen nachgewiesen werden, dass dieser Grenzwert überhaupt existiert Anschließend wurde der Satz zur Ableitung von f(x) = e x nachgewiesen Nachteil Viel Vorwissen über Folgen und Konvergenz (ist nicht mehr da)Definition 2 The exp function E(x) = ex is the inverse of the log function L(x) = lnx L E(x) = lnex = x, ∀x Properties • lnx is the inverse of ex ∀x > 0, E L = elnx = x • ∀x > 0, y = lnx ⇔ ey = x • graph(ex) is the reflection of graph(lnx) by line y = x • range(E) = domain(L) = (0,∞), domain(E) = range(L) = (−∞,∞) solve(exp(x)x = 0) gives ' LambertW(1)' intead of '056' which i found by simple fixed pt iteration how to find the root of 'exp(x)x = 0' tht gives the correct answer thanks




Exponential Function Wikipedia
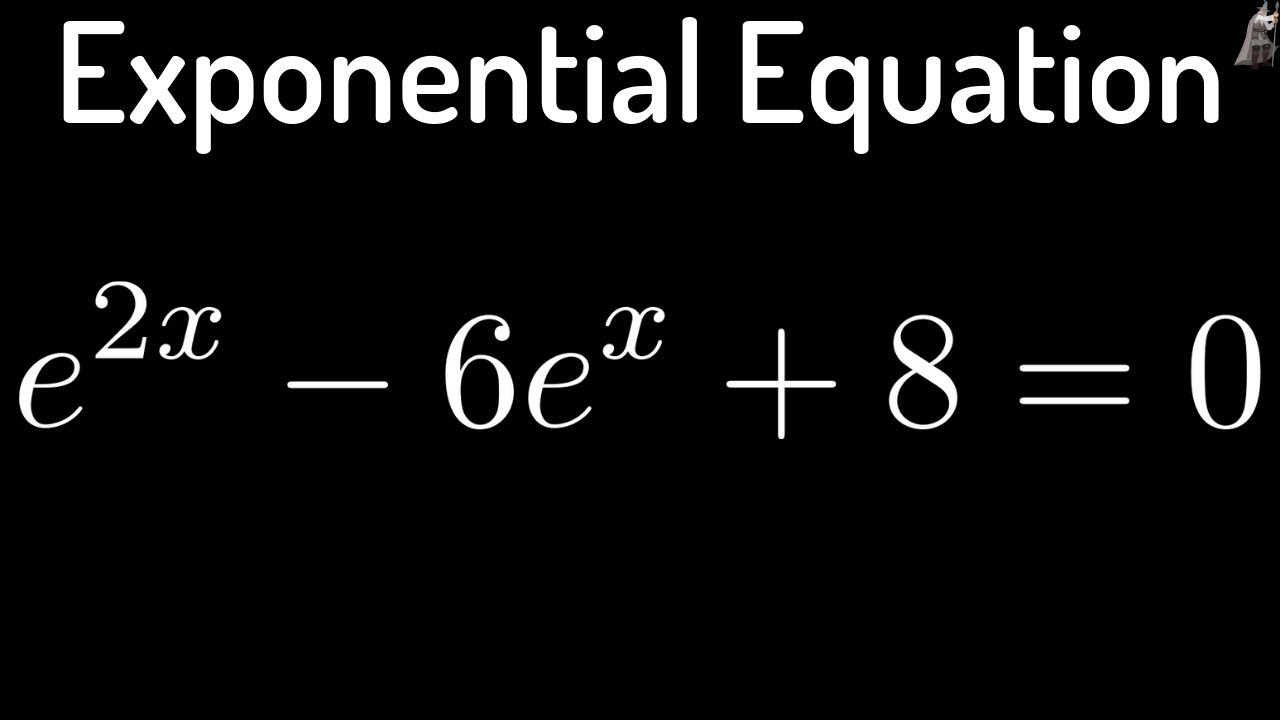



Solving The Exponential Equation E 2x 6 E X 8 0 Youtube
Falls jxj 6 1 N 2 ist (1) Wir beweisen die Stetigkeit von exp in Punkt x0Sei" > 0 Wir zeigen, dass ein > 0 existiert, f ur das die folgende Implikation giltZk, hat Konvergenzradius r = ∞, und daher ist exp(z)fu¨r alle z ∈ Cstetig Fu¨r reelle Argumente ist expR→Runendlich oft differenzierbar mit d dx exp(x)=exp(x), exp(0)=1 Anfangswertproblem fu¨r gewohnliche Differentialgleichung¨ Suche zu a ∈ Reine Funktion y(x)mit y′(x)=a ·y(x), y(x 0)=y 0 Die (eindeutige) Losung dieses Anfangswertproblems ist gegebenIstX(t) = exp(tA) X 0 Rt 0 exp −sA)G(s)ds!



Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf



Ocw Aprende Org Courses Mathematics 18 01sc Single Variable Calculus Fall 10 1 Differentiation Part B Implicit Differentiation And Inverse Functions Session 17 The Exponential Function Its Derivative And Its Inverse Mit18 01scf10 Ex17sol Pdf
• If 0 < X < ∞, then ∞< log(X) < ∞ You can't take the log of a negative number You can't take the log of a negative number • If ∞< X < ∞, then 0 < exp(X) < ∞N!1 1 wegen lim n!1x 2n= 0 AlsoE 0 = I;



1



Ocw Mit Edu Courses Economics 14 30 Introduction To Statistical Methods In Economics Spring 09 Assignments Mit14 30s09 Sol Pset06 Pdf
Sie heißt auch eFunktion und der Funktionsterm auch exp(x) Die Funktion mit f(x)=e x ist Thema dieser Webseite Graph top Der Graph geht durch den Punkt P(01) Er verläuft für x gegen Unendlich über alle Grenzen und für x gegen minus Unendlich gegen Null Die xAchse ist Asymptote Er ist echt monoton steigend Ein zweiter, markanter Punkt ist Q(1e) Eulersche ZahlThe calculator has a solver that allows him to solve a equation with exponential The calculations for obtaining the results are detailed, so it will be possible to solve equations like `exp(x)=2` or like `exp(2*x4)=3` or like `exp(x^21)=1` with Übrigens kann man auch mit dem Zwischenwertsatz argumentieren Gäbe es ein x mit exp (x)0 und der Stetigkeit von exp (x) auch ein x mit exp (x)=0, im Widerspruch zu exp (x)exp (x)=1




Ex 6 2 19 The Interval In Which Y X2 E X Is Increasing
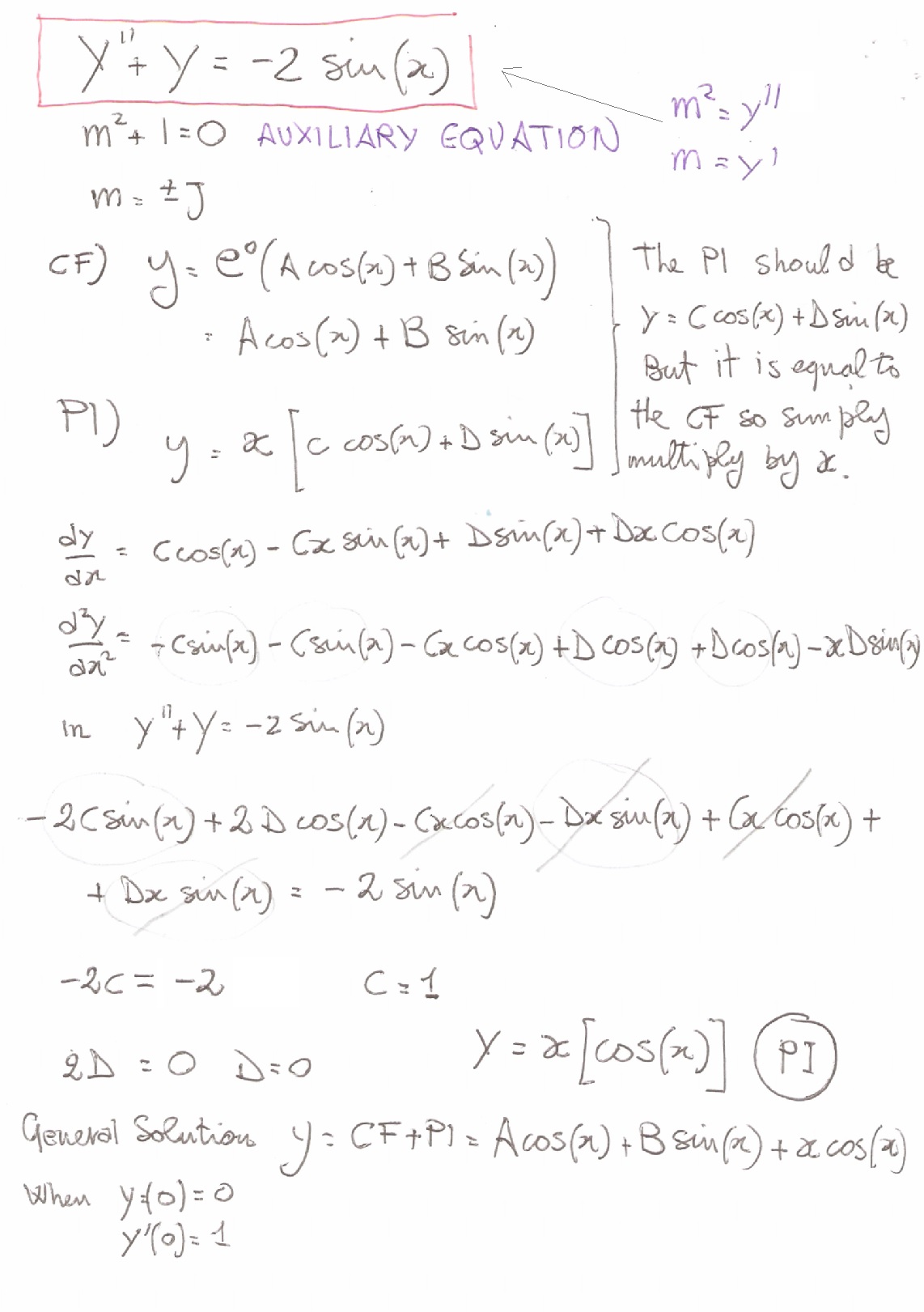



How Do I Solve Y Y 2 Sin X With The Initial Conditions Y 0 0 And Y 0 1 Socratic
Dieser Artikel steht unter einer freien CCBYSA 30 Lizenz Damit kannst du ihn frei verwenden, bearbeiten und weiterverbreiten, solange du „Mathe für NichtFreaks" als Quelle nennst und deine Änderungen am Text unter derselben CCBYSA 30 oder einer dazu kompatiblen Lizenz stellstWir benutzen die Konvexit¨at der Exponentialfunktion, d h dass f ¨ur alle x,y ∈ R und λ ∈ 0,1 gilt exp (1−λ)xλy 6 (1−λ)exp(x)λexp(y) (∗) Seien ohne Einschr¨ankung A,B > 0 W¨ahle x = lnA, y = lnB und λ = 1 q Wegen q > 1 ist λ ∈ 0,1 Außerdem gilt 1−λ = 1 p 1 q − 1 q = 1 p Wir erhalten A1/pB1/q = exp ln(A1/p) exp ln(B1/q) = exp 1 p lnA 1 q lnB (∗Exp(x) = X n≥0 1 n!



Http Tyr0 Chem Wsu Edu Kipeters Chem332 Resources Tableofusefulintegrals Pdf




At What Values Of X Does F X 0 Brainly Com
(d) Asymptotisches Verhalten f¨ur x→ ±∞ lim xHierbei ist P 1 k=0 a k absolut konvergent L osungsvorschlag zu a) (i) Ist jxj1, dann ergibt sich f n(x) = x2n 1 x 2n = 1 1 x!Rithmus" ln (0,∞) 7→R nennt ln(exp(x)) = x fur alle¨ x ∈ R , exp(ln(y)) = y f¨ur alle y ∈ (0,∞) Beispiel 53 Durch Spiegelung an der Winkelhalbierenden ergibt sich sofort der Graph von ln aus dem Graphen von exp >> plotfunc2d(x, exp(x), ln(x), x = 44, ViewingBox = 44, 44) Da die Exponentialfunktion nach Satz 414 monoton und stetig ist, ist mit Satz 433 auch der




The Equation Log E X Log E 1 X 0 Can Be Written As




13 Limits At Infinity Example With E 1 X Youtube
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledgeX5 Leitfaden 64 (Wenn wir die rechte Seite mit g(x) bezeichnen, also g(x) = P n≥0 1 n!x n, so stellt man als erstes fest, dass diese unendlichen Summen f¨ur alle reelle Zahlen x wirklich reelle Zahlen liefern (man sagt, dass die Reihe konvergiert) Funktionen, die durch derartige konvergente Reihen gegeben sind, sind@2g @y2 (x;y) = ( 24y 2 32x 2 2)exp( 3x 4y) ( 8y 32xy 2y)exp( x2 4y2)8y = (64y4




The Solution Of The Differential Equation Dy Dx 1 E X Y Is A X Y E X Y 0 B X C E X Y 0 C X C E X Y 1 D X C E X Y 1 0




Statement 1 The Equation E X 1 X 2 0 Has Only One Real Root Statement 2 Between Any Two Root Of An Equation F X 0 There Is A Root Of Its Derivative F X 0
(c) exp(x) >0f¨ur alle x∈R; Hallo, es geht um folgende Aufgabe Zeigen Sie, dass exp(x) > 0 für alle x ∈ ℝGehen Sie dabei wie folgt vor i) Zeigen Sie zunächst, dass exp(x)*exp(x)=1 für alle x ∈ ℝ, indem Sie die Ableitung von g (x) = exp(x)*exp(x) betrachten ii) Überlegen Sie nun, dass exp(x) ≠ 0 für alle x ∈ ℝ iii) Zeigen Sie schließlich, dass die Annahme exp(x) < 0 für irgendein x ∈ ℝ zumThis function, also denoted as exp x, is called the "natural exponential function", or simply "the exponential function" Since any exponential function can be written in terms of the natural exponential as = , it is computationally and conceptually convenient to reduce the study of exponential functions to this particular oneThe natural exponential is hence denoted by



What Is The Value Of Math Lim Limits X To 0 Frac E Sin X 1 X Math Quora




For The Following Differential Equation D 2y Dx 2 Chegg Com



Http Www Isye Gatech Edu Sman Courses 6739 T3su15solns Pdf




Elements Of Analysis




Lim X Tends To 0 1 X 1 X E X Is Equal To Brainly In
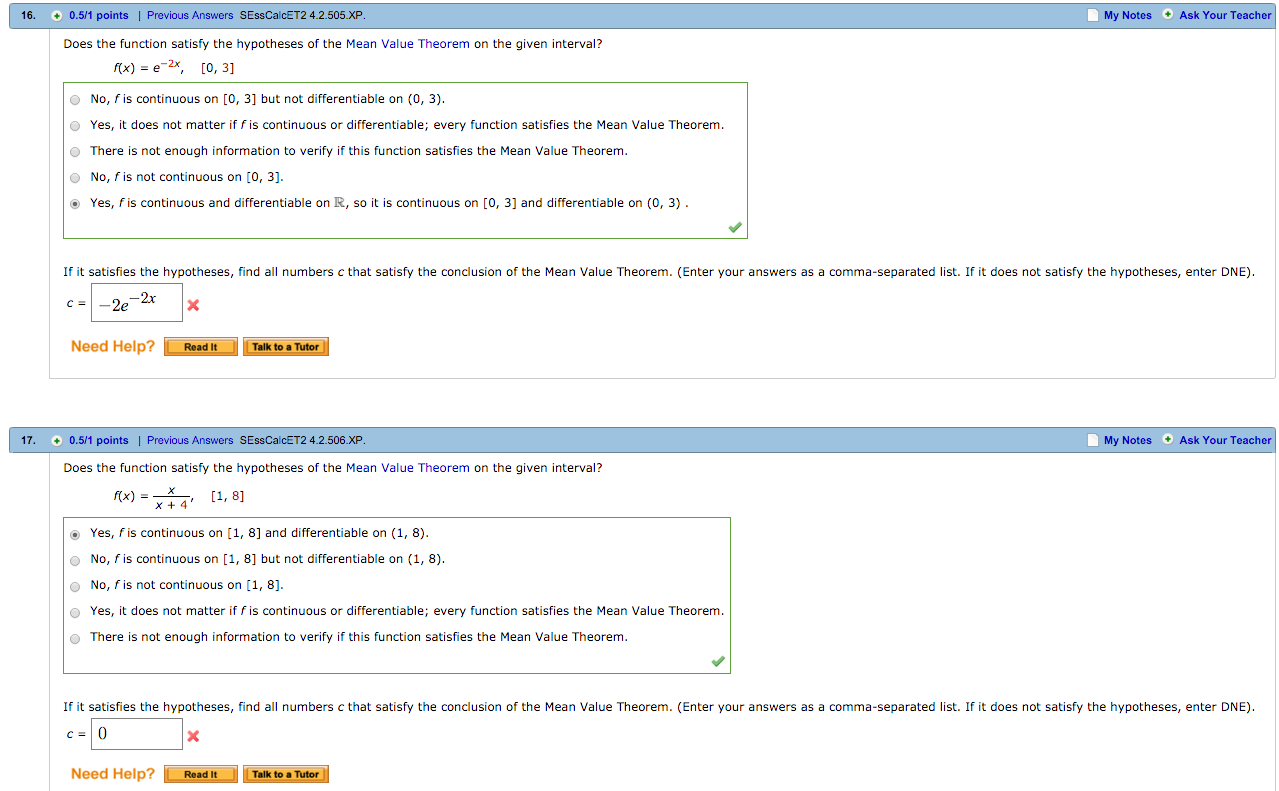



Does The Function Satisfy The Hypotheses Of The Mean Chegg Com



Web Northeastern Edu Alina Hw3 Solutions Pdf




Newton S Method And Its Extensions Ppt Download




Limit Of 1 X 1 X As X Approaches 0 Youtube



Math Msu Edu Classes Mth 299 Mth 299 Waiver Example Problems Pdf




Ex 9 4 5 Find General Solution Ex E X Dy Ex E X Dx



Expansion Of E X




Fallsem 21 Mat01 Eth Vl Reference Material I 15 Jul Mat01 Se Book Module 1 1 Pages 351 400 Flip Pdf Download Fliphtml5




Engineering Mathematics Notes
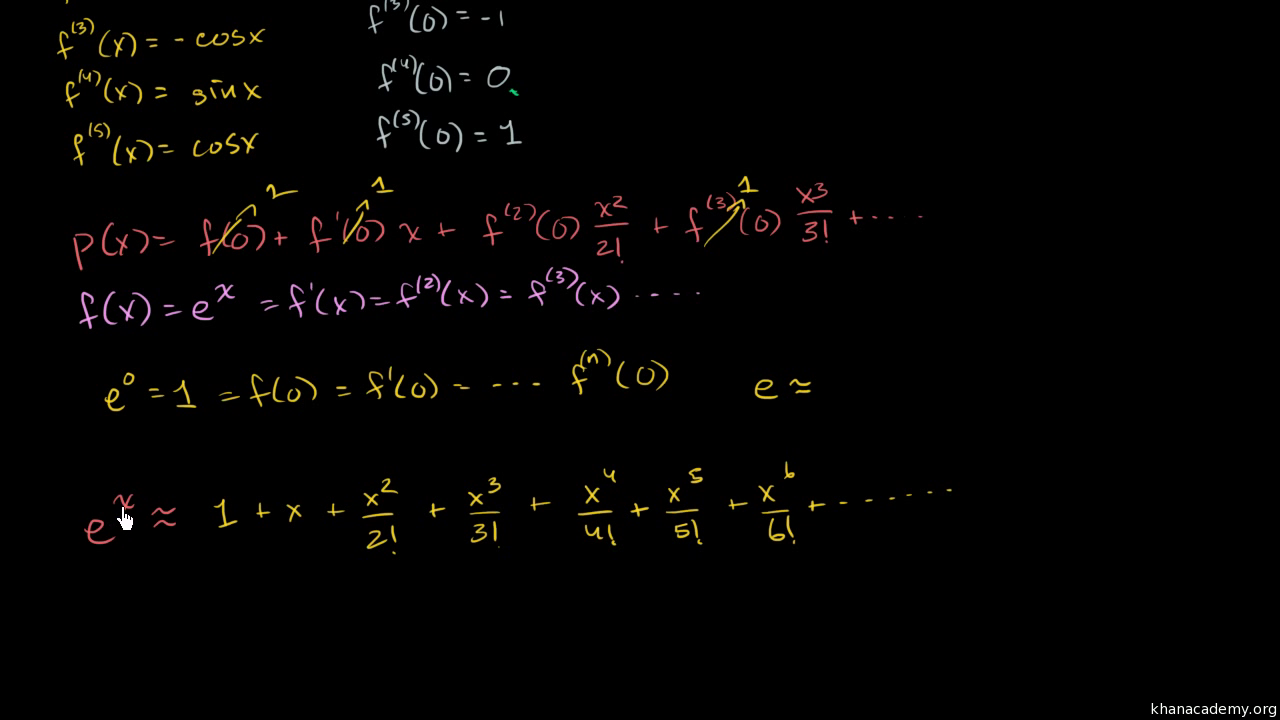



Maclaurin Series Of Eˣ Video Khan Academy




Evalute The Value Of Limit Mathematics Stack Exchange




Lim X Tends To 1 E X E X 1 Please Fast Experts Maths Limits And Derivatives Meritnation Com




Maclaurin And Taylor Series Ppt Download




What Is The Maximum Likelihood Estimator For E Theta P X I 0 Cross Validated



1



E X As A Limit Youtube




Taylor Polynomial For E X About X 0 Youtube




Elements Of Analysis



Www Stat Auckland Ac Nz Fewster 210 Notes 16s2 Ch4annotated Pdf




The Improper Integral Of E X From 0 To Infinity Youtube




The Random Variable X The No Of Defective Items When Three Electronic Components Are Tested Would Be Pdf Free Download
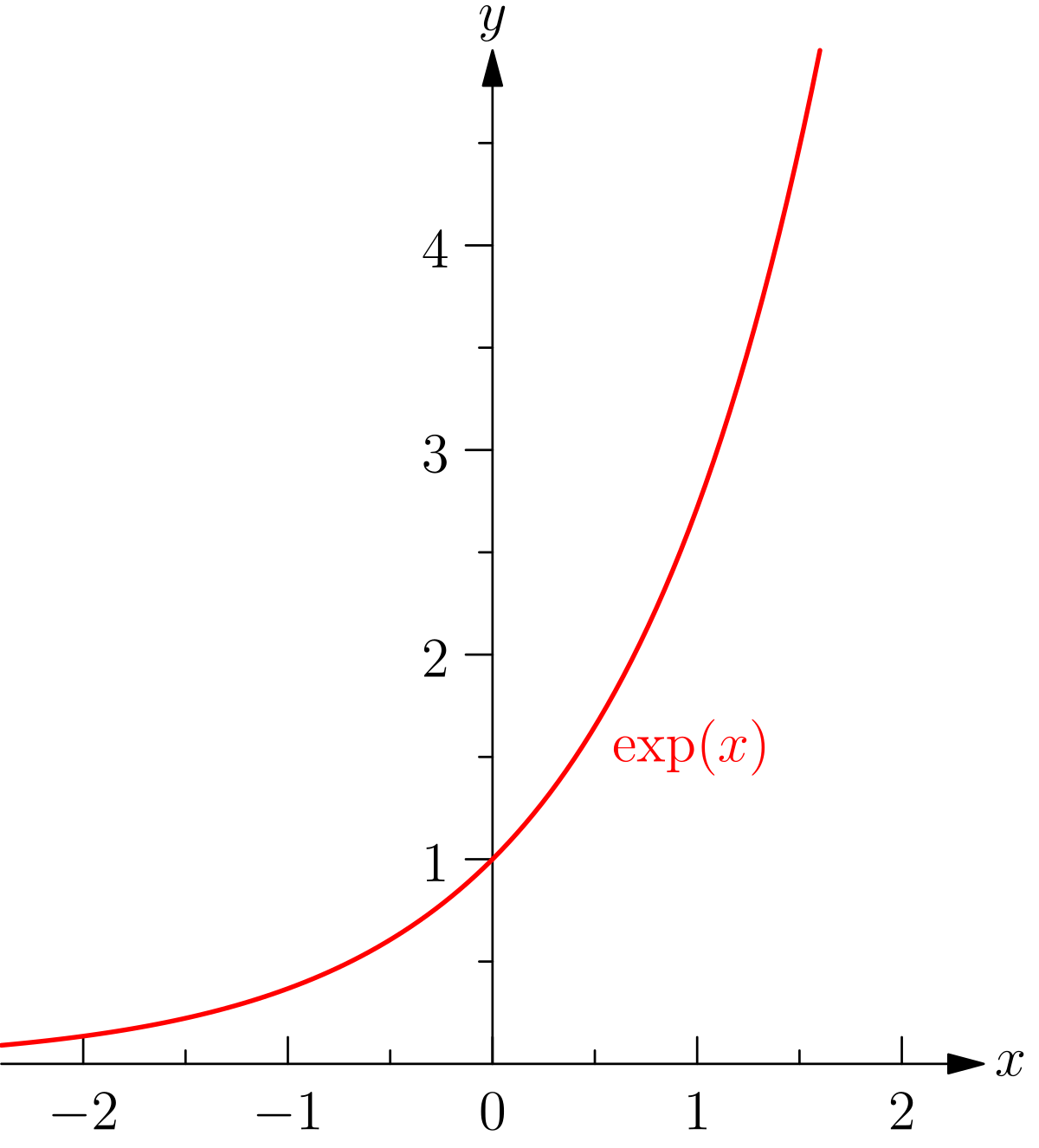



File Mfnf Exp Svg Wikimedia Commons



Http Users Math Msu Edu Users Gnagy Teaching 12 Spring Mth133 L06 133 Pdf



Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf




Misc 9 Find Particular Solution 1 E2x Dy 1 Y2 Ex



Hug Scholar Insignificant Lim Exp Berkgruptemizlik Com




Solve X 3 2y 3 Dx 3xy 2dy 0



Stanford Edu Jduchi Projects Probability Bounds Pdf
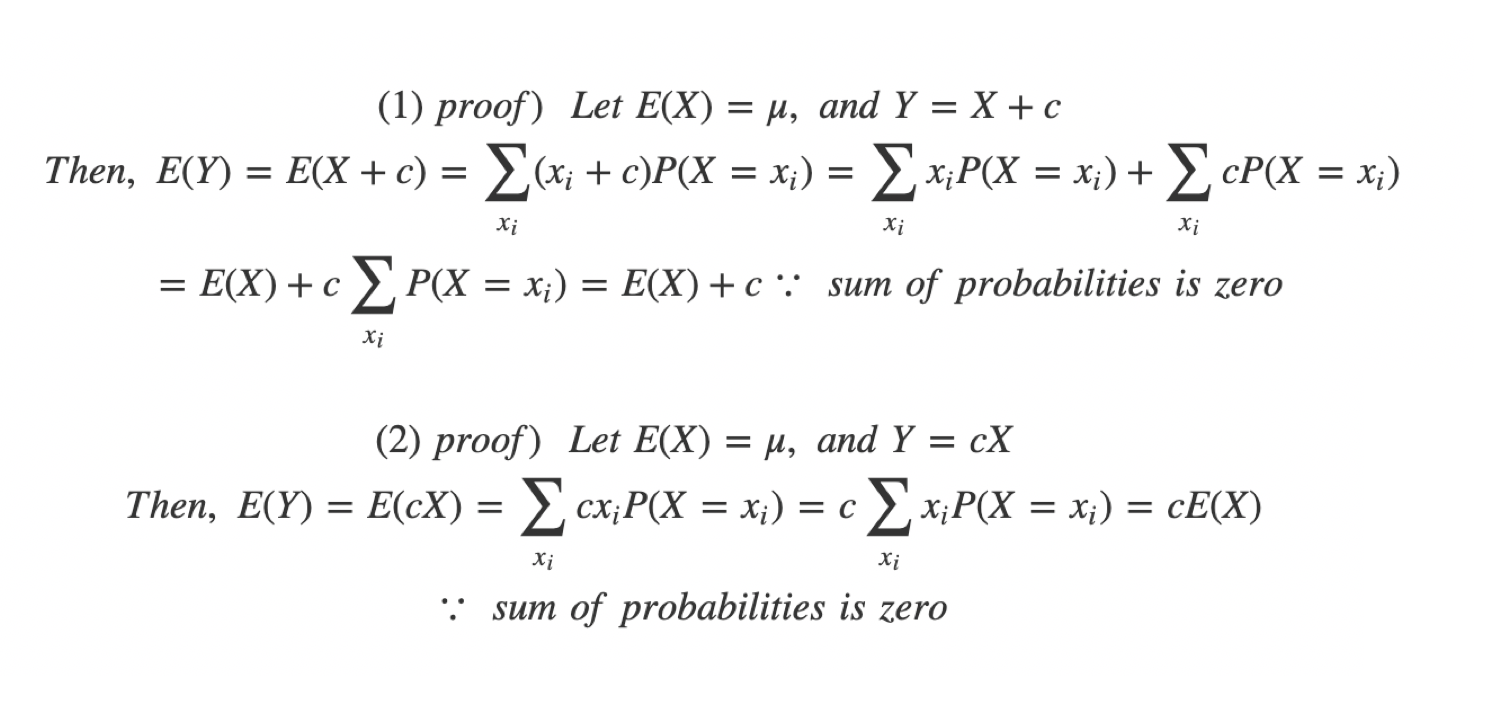



Data Science 1 Expectation Variance Law Of Large Numbers By Jun Jun Devpblog Medium



Http Www Isye Gatech Edu Sman Courses 6739 T3su17solns Pdf




E Mathematical Constant Wikipedia




Prove That 1 X E X 1 Xe X X 0




How Do You Find The Equation Of The Tangent To The Curve Defined By Y 2e X 1 E X At The Point 0 1 Socratic
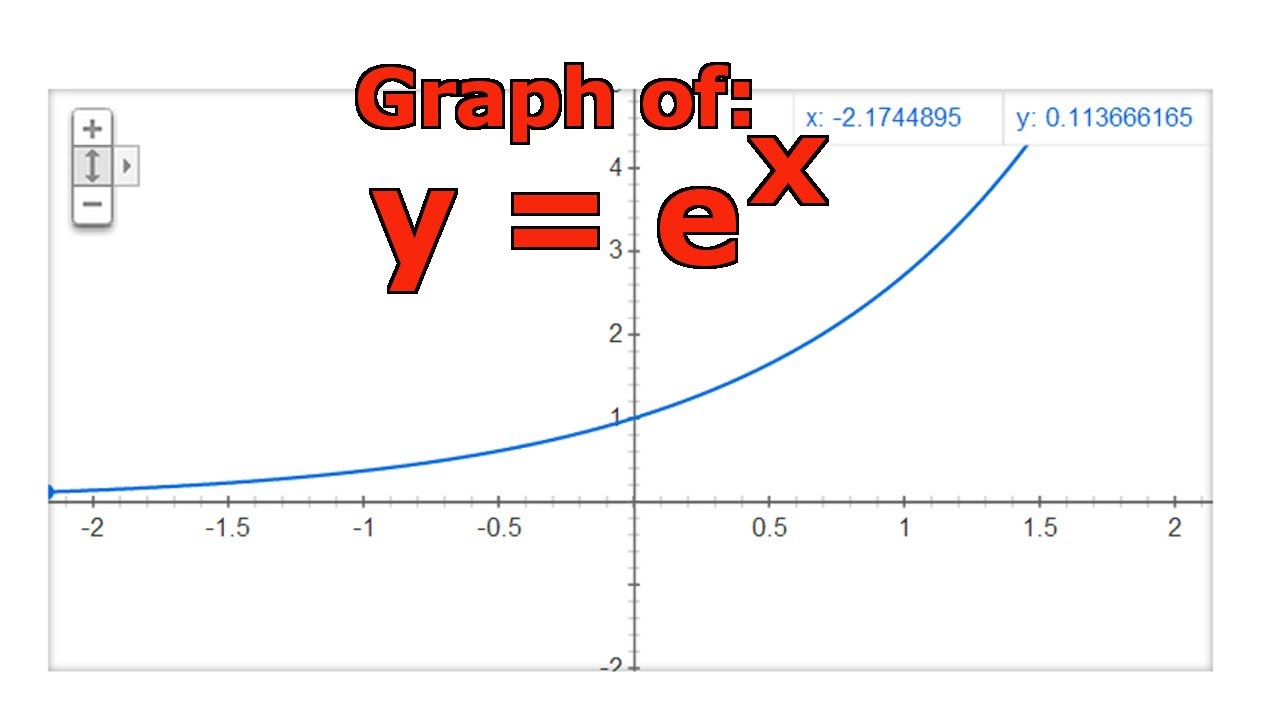



Graphing The Natural Exponential Function Y E X Youtube




Chapter 6 Functions Of Random Variables Question 2




1 Find The Fourier Integral Representation Of F X Chegg Com
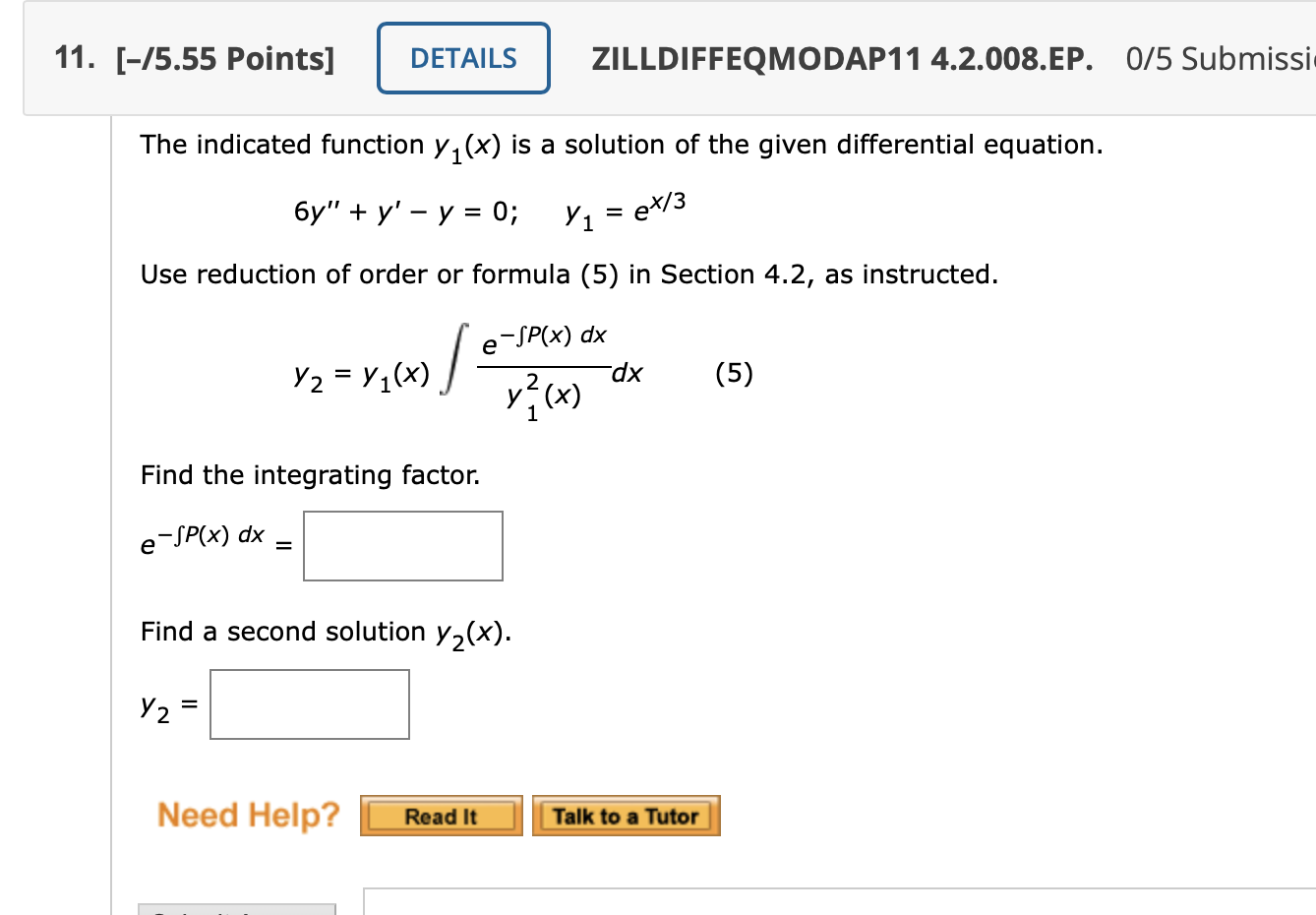



The Indicated Function Y1 X Is A Solution Of The Chegg Com




Fallsem 21 Mat01 Eth Vl Reference Material I 15 Jul Mat01 Se Book Module 1 1 Pages 351 400 Flip Pdf Download Fliphtml5



1




Question Video Finding The Linear Approximation Of An Exponential Function To Estimate An Exponential Value Nagwa




Proof Of E As A Limit Mathematics Stack Exchange




Proof The Derivative Of 𝑒ˣ Is 𝑒ˣ Video Khan Academy




Theta Function Wikipedia
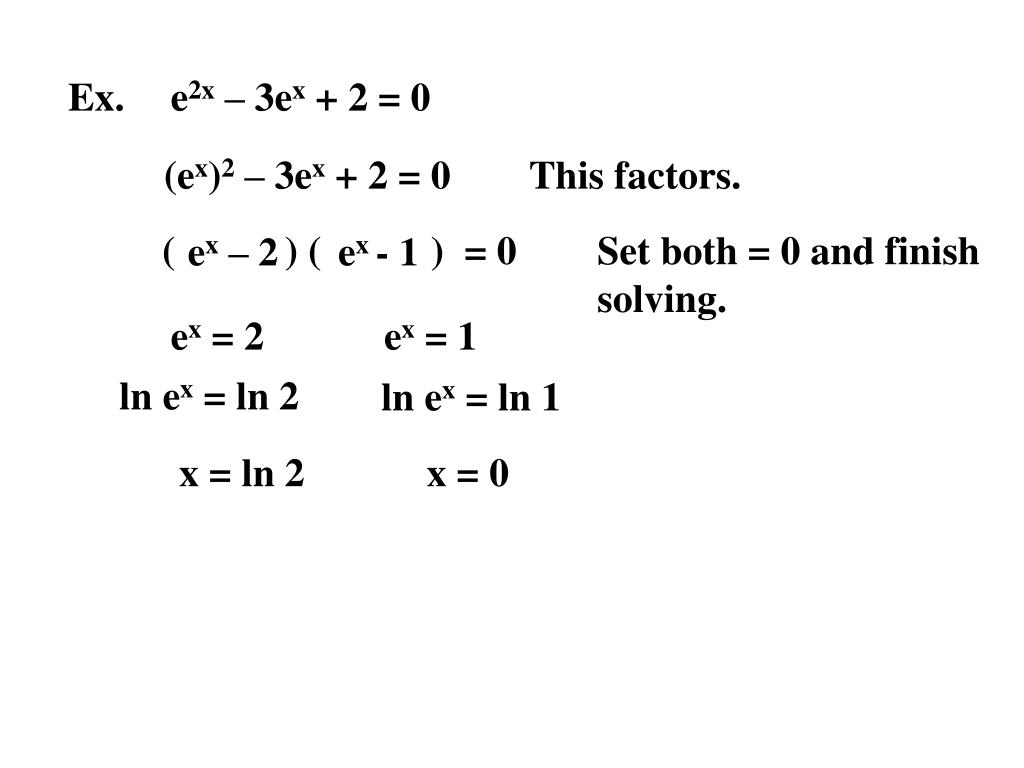



Ppt 3 4 Exponential And Logarithmic Equations Powerpoint Presentation Id




Misc 35 Prove Definite Integral 0 1 X Ex Dx 1 Miscellaneous




Show Limit Does Not Exist As X Approaches Zero For E 1 X Youtube



Cochranmath Taylor Series Of A Function By Equating Derivatives




Solve D 3y Dx 3 3 D 2y Dx 2 3 Dy Dx Y E X 2 Mathematics 2 Question Answer Collection



Www Colorado Edu Amath Sites Default Files Attached Files Hw5sol 5 Pdf



2




Limits Of Transendental Function E 1 X 1 E 1 X 1 As X Approaches Zero Test 1 Youtube




Natural Logarithm Function Ppt Download



Www Wssd K12 Pa Us Downloads Ap calculus exam prep assign11p1key Pdf




Find A Real Root Of The Equation X E X Using The Newton Rapshon Method Mathematics 3 Question Answer Collection



Ocw Mit Edu Courses Economics 14 30 Introduction To Statistical Methods In Economics Spring 09 Assignments Mit14 30s09 Sol Pset06 Pdf




Expected Value Of A Binomial Variable Video Khan Academy



Solved Y 6y 11y 6y 0 Differential Equation Does Have 2 Solutions Y1 X E X And Y2 X E 2x Investigate The Given Y X C1e X C2 Course Hero



Solved Y 6y 11y 6y 0 Differential Equation Does Have 2 Solutions Y1 X E X And Y2 X E 2x Investigate The Given Y X C1e X C2 Course Hero




Mean Expected Value Of A Discrete Random Variable Video Khan Academy




Help In Proving That Int 0 Infty Frac 1 Gamma X D X E Int 0 Infty Frac E X Pi 2 Ln X 2 D X Using Real Methods Only Mathematics Stack Exchange




How Do You Determine The Maximum And Minimum Value Of The Function F X Xe X 2 Socratic



Faculty Math Illinois Edu R Ash Stat Statsols Pdf



Faculty Math Illinois Edu Hildebr 370 408discrete1 Pdf




Discuss The Continuity Of F X E X 1 Log 1 2x X Not Equal To Zero 7 When X 0 At X 0 Brainly In




Natural Logarithm Function Ppt Download



0 件のコメント:
コメントを投稿